
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Степенные ряды
|
|
Число 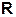 называется радиусом сходимостистепенного ряда, если при всех
называется радиусом сходимостистепенного ряда, если при всех  , для которых
, для которых  , степенной ряд сходится, а при всех
, степенной ряд сходится, а при всех  , для которых
, для которых 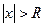 , степенной ряд расходится.
, степенной ряд расходится.
Радиус сходимости вычисляется по формуле:
 .
.
Промежуток 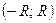 называют интервалом сходимостистепенного ряда.
называют интервалом сходимостистепенного ряда.
Область сходимостистепенного ряда либо совпадает с его интервалом сходимости, либо получается из этого интервала добавлением одной или обеих граничных точек, т. е.  и
и  .
.
Пример 53.
Найти радиус и область сходимости степенного ряда  .
.
Решение.
1) Воспользуемся формулой для нахождения радиуса сходимости:
 ,
, 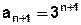 ,
,
 .
. 
Таким образом, радиус сходимости равен  .
.
2) Интервал сходимости этого ряда  . Исследуем сходимость этого ряда на концах интервала.
. Исследуем сходимость этого ряда на концах интервала.
3)  , получим числовой ряд
, получим числовой ряд  .
.
Данный ряд расходится.
4)  , получим числовой ряд
, получим числовой ряд  . Данный ряд расходится.
. Данный ряд расходится.
5) Значит интервал сходимости данного ряда  .
.
Пример 54.
Найти область сходимости степенного ряда  .
.
Решение.
1) Найдем радиус сходимости ряда:  ,
,  ,
, 
 . Радиус сходимости
. Радиус сходимости 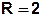 .
.
2) Интервал сходимости равен промежутку  .
.
3) Найдём область сходимости. Для этого надо исследовать поведение ряда в точках  и
и 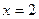 .
.
a)  . Наш ряд примет вид
. Наш ряд примет вид  .
.
По признаку Лейбница данный ряд сходится, т. к. все члены ряда по абсолютной величине монотонно убывают (1; 0,5; 0,333; 0,25; 0,2; …) и общий член стремится к нулю  .
.
Значит, точку  включаем в область сходимости.
включаем в область сходимости.
b) 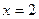 . Получим расходящийся гармонический ряд
. Получим расходящийся гармонический ряд  .
.
Значит, точку 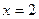 не включаем в область сходимости.
не включаем в область сходимости.
Таким образом, областью сходимости будет промежуток  .
.
Пример 55.
Найти область сходимости степенного ряда  .
.
Решение.
1) Сделаем подстановку  . Получим ряд
. Получим ряд  Найдем радиус сходимости этого ряда:
Найдем радиус сходимости этого ряда:  ,
,  ,
, 
 . Радиус сходимости
. Радиус сходимости  .
.
2) Интервал сходимости ряда  равен промежутку
равен промежутку  , Найдём область сходимости этого ряда.
, Найдём область сходимости этого ряда.
Найдём область сходимости. Для этого надо исследовать ряд в точках  и
и  .
.
a)  .
.
Наш ряд примет вид  .
.
Все члены ряда по абсолютной величине монотонно убывают (1; 0,25; 0,111; 0,063; 0,04; …) и общий член стремится к нулю  .
.
По признаку Лейбница данный ряд сходится, значит, точку  включаем в область сходимости.
включаем в область сходимости.
b)  .
.
Получим сходящийся гармонический ряд  .
.
Значит, точку  включаем в область сходимости.
включаем в область сходимости.
Таким образом, областью сходимости ряда  будет промежуток
будет промежуток  .
.
3) Вернёмся к переменной х 
Таким образом, областью сходимости будет промежуток  .
.
Литература:
[1] стр. 392-400, [2] стр. 431-446, [3] стр. 414-416, [5] стр. 391-396
Date: 2015-10-19; view: 433; Нарушение авторских прав