Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример 49
|
|
Исследовать на сходимость знакочередующийся ряд 
. Если ряд сходится, то определить, сходится он абсолютно или условно.
Решение.
Применим теорему Лейбница.
1) Все члены ряда по абсолютной величине монотонно возрастают: 0,1; 1; 1,441; 1,655; 1,768; …..
2) Общий член ряда стремится к 2:
.
Таким образом, условия теоремы Лейбница не выполняются и, значит, знакочередующийся ряд расходится.
Пример 50
Исследовать на сходимость знакочередующийся ряд 
. Если ряд сходится, то определить, сходится он абсолютно или условно.
Решение.
1) Применим теорему Лейбница.
a) Все члены ряда по абсолютной величине монотонно убывают: 0,667; 0,429; 0,316; 0,25; 0,207; ….
b) Общий член ряда стремится к нулю: 
.
Значит, по теореме Лейбница знакочередующийся ряд сходится.
2) Составим соответствующий знакочередующемуся ряду положительный ряд
.
3) Применим признак Коши. 
.
Значит, по признаку Коши ряд сходится.
4) Таким образом, знакочередующийся ряд абсолютно сходится.
Пример 51.
Исследовать на сходимость знакочередующийся ряд 
. Если ряд сходится, то определить, сходится он абсолютно или условно.
Решение.
1) Применим теорему Лейбница.
a) Все члены ряда по абсолютной величине монотонно убывают: 0,32; 0,053; 0,021; 0,011; 0,007115; ….
b) Общий член ряда стремится к нулю: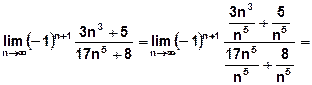 
.
Значит, по теореме Лейбница знакочередующийся ряд сходится.
2) Составим соответствующий знакочередующемуся ряду положительный ряд
.
3) Рассмотрим сходящийся обобщённо -гармонический ряд 
. Применим предельный признак
сравнения: 
.
Значит, по предельному признаку сравнения ряд сходится.
4) Таким образом знакочередующийся ряд абсолютно сходится.
Пример 52.
Исследовать на сходимость знакочередующийся ряд 
. Если ряд сходится, то определить, сходится он абсолютно или условно.
Решение.
1) Применим теорему Лейбница.
a) Все члены ряда по абсолютной величине монотонно убывают: 2; 2; 1,333; 0,667; 0,267; ….
b) Общий член ряда стремится к нулю: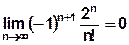 
.
Значит, по теореме Лейбница знакочередующийся ряд сходится.
2) Составим соответствующий знакочередующемуся ряду положительный ряд 
.
3) Применим признак Даламбера. 
. 
.
Значит, по признаку Даламбера ряд сходится.
4) Таким образом знакочередующийся ряд абсолютно сходится.
Литература:
[1] стр. 386-390, [2] стр. 420-424, [3] стр. 410-414, [5] стр. 389-391
Date: 2015-10-19; view: 363; Нарушение авторских прав