Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример 42
|
|
Выполняется ли необходимый признак сходимости у ряда 
.
Решение.Вычислим
. 
Так как, общий член стремится к нулю, то выполняется необходимый признак сходимости ряда.
3.1.2 Признаки сходимости рядов с неотрицательными членами
Теорема (Признак сравнения рядов). Пусть даны два положительных ряда:
Если для всех достаточно больших n 
, то:
1) из сходимости ряда 
следует сходимость ряда 
и сумма ряда не превосходит суммы ряда ;
2) из расходимости ряда следует сходимость ряда .
Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого заведомо сходящегося ряда.
Исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящегося ряда.
Следствие (Предельный признак сравнения). Если для положительных рядов
существует конечный
то эти ряды сходятся или расходятся одновременно.
Для сравнения обычно используют геометрический и гармонический ряды.
Пример 43.
Используя признак сравнения рядов исследовать сходимость ряда 
.
Решение.
Сравним данный ряд с расходящимся обобщённо гармоническим рядом 
(
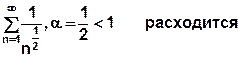). У нашего ряда 
, а у обобщённого гармонического 
. Имеем 
. Следовательно, по признаку сравнения рядов наш ряд расходится.
Пример 44 .
Используя предельный признак сравнения рядов исследовать сходимость ряда 
.
Решение.
Сравним данный ряд со сходящимся обобщённо гармоническим рядом 
(
).
У нашего ряда n - ыйчлен 
, а у сходящегося - 
. Найдём r:
.
Разделим числитель и знаменатель на n2
.
Таким образом, 
. Значит по предельному признаку сравнения ряд сходится.
Вопрос о сходимости рядов вида 
, где 
- многочлен от n степени k, a 
- многочлен от n степени l, полностью исчерпывается сравнением с рядом 
, где 
. Удобнее при этом использовать признак сравнения в предельной форме.
Пример 45.
Используя предельный признак сравнения рядов исследовать сходимость ряда 
.
Решение.
1)В данном случае l=5, k=3,отсюда 
. Сравнивать будем с рядом , т.к. 
, то он сходится.
2) Вычислим 
, значит данный ряд также сходится.
Теорема (Признак Даламбера). Если члены положительного ряда таковы, что существует предел 
, то при 
ряд сходится, а при 
ряд расходится.
Замечание. При 
признак Даламбера ответа не даёт.
Пример 46.
С помощью признака Даламбера исследовать сходимость ряда 
.
Решение.
n – ый член ряда равен 
. Найдем (n+1) – ый член ряда. Для этого вместо n запишем выражение n+1: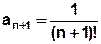 
.
Применим признак Даламбера
.
Воспользуемся свойством факториалов, получим
.
Таким образом, 
. Значит, по признаку Даламбера ряд 
сходится.
Теорема (Признак Коши). Если члены положительного ряда таковы, что существует предел 
, то при 
ряд сходится, а при 
ряд расходится.
Замечание 2. При 
признак Коши ответа не даёт.
Пример 47.
С помощью признака Коши исследовать сходимость ряда 
.
Решение.
n – ый член ряда равен 
. Применим признак Коши
.
Таким образом, 
. Значит, по признаку Коши ряд сходится.
Литература:
[1] стр. 377-386, 74-76 [2] стр. 396-415, [3] стр. 397-410, [5] стр. 379-388
Date: 2015-10-19; view: 466; Нарушение авторских прав