Линейные однородные дифференциальные уравнения второго

порядка с постоянными коэффициентами

Для решения таких уравнений удобно пользоваться таблицей:

Дифференциальное уравнение
Характеристическое уравнение
Дискриминант	D>0	D=0	D<0
Корни характеристического уравнения	k1≠k2	k1=k2=k	k1=a+bi k2=a-bi
Общее решение дифференциального уравнения

Пример 34

Решите уравнение:

.

Решение:

1) Запишем характеристическое уравнение

2) Найдём его корни

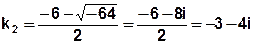
3) Запишем общее решение:

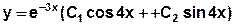
4) Ответ:

Пример 35

Решите уравнение:

Решение:

1) Запишем характеристическое уравнение

2) Найдём его корни

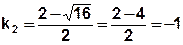
3) Запишем общее решение:

4) Найдём частное решение, для этого найдём

Подставим начальные условия

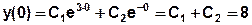
Запишем полученные условия в виде системы и решим её

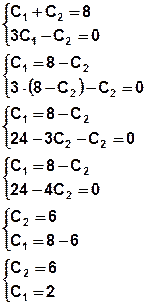
5) Запишем частное решение:

Ответ:

Date: 2015-10-19; view: 316; Нарушение авторских прав