
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проверка решения в среде MathCad. Для начала работы нам понадобится представление , в нашей задаче это
|
|
Для начала работы нам понадобится представление  , в нашей задаче это
, в нашей задаче это  .
.
Запись произведём с помощью значка «:=» на панели «Вычисления» или «Калькулятор».
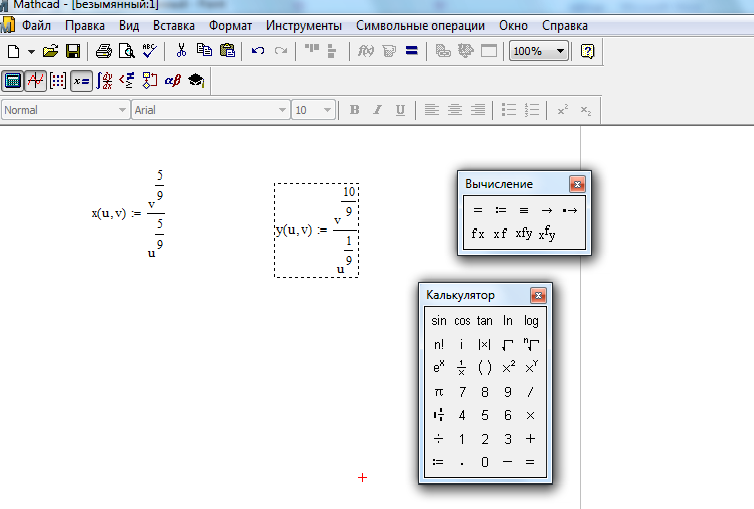
Рисунок 2.8
Затем откроем панель инструментов “ f(x)” («Вставить функцию»). В левом столбце выбираем категорию функции – «Решение дифференциального уравнения», в правом столбце находим функцию Jacob и нажимаем кнопку «ОК».

Рисунок 2.9
Аргументы функции Jacob - две матрицы, записанные через запятую.
Первая матрица-столбец – это определённые ранее функции  и
и  , вторая – матрица-столбец, состоящая из переменных, по которым будет произведено дифференцирование, в нашей задаче это
, вторая – матрица-столбец, состоящая из переменных, по которым будет произведено дифференцирование, в нашей задаче это  . Задать матрицу требуемого размера можно с помощью кнопки на панели «Матрица».
. Задать матрицу требуемого размера можно с помощью кнопки на панели «Матрица».

Рисунок 2.10
Если далее на панели «Вычисления» выбрать значок  , программа выведет на экран матрицу Якоби. Чтобы вычислить её определитель, Якобиан, на панели «Матрица» нажмём на кнопку
, программа выведет на экран матрицу Якоби. Чтобы вычислить её определитель, Якобиан, на панели «Матрица» нажмём на кнопку  , вместо х вставим предыдущую запись.
, вместо х вставим предыдущую запись.

Рисунок 2.11
Осталось записать двойной интеграл и сверить полученное нами и вычисленное компьютером значение площади области  . Как видим, ошибки нет.
. Как видим, ошибки нет.

Рисунок 2.12
Занятие 3.
Вычисление объемов тел с помощью двойного интеграла. Вычисление площади поверхности в декартовых координатах с помощью двойного интеграла.
Ауд.: ОЛ-6 №№2198, 2200, 2203, 2219, 2214, 2216 или ОЛ-5 №№8.69, 70, 76, 85, 86, 88
1. Вычисление объемов тел с помощью двойного интеграла.
 С помощью двойного интеграла можно вычислить объём тела, ограниченного цилиндрической поверхностью, параллельной оси
С помощью двойного интеграла можно вычислить объём тела, ограниченного цилиндрической поверхностью, параллельной оси  , опирающегося на область
, опирающегося на область  в плоскости
в плоскости  , и ограниченного сверху поверхностью
, и ограниченного сверху поверхностью 
(см. геометрический смысл двойного интеграла, см. рис. 3.1).
| Рисунок 3.1 |
 , если
, если  (3.1)
(3.1)

| Рисунок 3.2 |
 , а снизу
, а снизу  , то его объём вычисляется по формуле
, то его объём вычисляется по формуле
 (3.2)
(3.2)
(См. рис. 3.2)
Пример 3.1 (2200) Найдём объём тела, ограниченного поверхностями:

Решение. На рис. 3.3 изображено тело, ограниченное заданными плоскостями. Оно представляет собой пирамиду, сверху ограниченную плоскостью  , снизу – плоскостью
, снизу – плоскостью  .
.
По бокам тело ограничивают вертикальные плоскости  ,
,  , и
, и 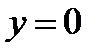 . Изображённая в правой части рисунка область D – проекция тела на плоскость XOY, которая является x – правильной.
. Изображённая в правой части рисунка область D – проекция тела на плоскость XOY, которая является x – правильной.

Рисунок 3.3
Вычислим объём данного тела с помощью формулы (3.1):
 .
.
Область  изображена на рис. 3.3, тело сверху ограничено плоскостью
изображена на рис. 3.3, тело сверху ограничено плоскостью  , т.е.
, т.е.  . Подставим эту функцию в двойной интеграл. Для всех точек области
. Подставим эту функцию в двойной интеграл. Для всех точек области  переменные заключены в пределах
переменные заключены в пределах  и
и  . Перейдём к повторному интегралу и, расставив пределы интегрирования, вычислим его.
. Перейдём к повторному интегралу и, расставив пределы интегрирования, вычислим его.  .
.
Пример 3.2 Вычислим с помощью двойного интеграла объём тела, ограниченного плоскостью  , параболоидом
, параболоидом  и двумя цилиндрами
и двумя цилиндрами  .
.
Решение. На рис. 3.4 изображено тело, ограниченное заданными поверхностями. Спроецируем его на координатную плоскость XOY.

Рисунок 3.4
Полученная проекция представляет собой область  , заключённую между двумя окружностями.
, заключённую между двумя окружностями.
Цилиндрическое тело опирается на эту область и ограничено сверху поверхностью  .
.
Составим двойной интеграл для вычисления объёма этого тела, по формуле (3.1):  .
.
Исходя из вида подынтегральной функции и области D, делаем заключение, что данный интеграл удобнее вычислять в полярных координатах.
Учитывая симметричность тела относительно плоскости  , вычислим объём той части тела, которая расположена в первом октанте, и удвоим его.
, вычислим объём той части тела, которая расположена в первом октанте, и удвоим его.
Область интегрирования при этом ограничена так, что  .
.
Перейдём к повторному интегралу и вычислим его.
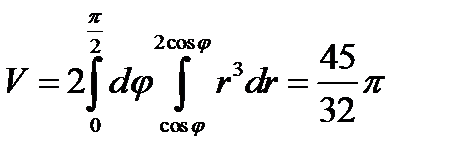 .
.
Замечание 1. Если тело ограничено двумя поверхностями, имеющими уравнения  и
и  , то чтобы составить уравнение цилиндра, в котором это тело заключено и который проецирует его на плоскость
, то чтобы составить уравнение цилиндра, в котором это тело заключено и который проецирует его на плоскость  , необходимо из системы этих уравнений исключить переменную
, необходимо из системы этих уравнений исключить переменную  . (См.рис.3.2)
. (См.рис.3.2)
 При этом уравнение полученного цилиндра
При этом уравнение полученного цилиндра  совпадает с уравнением границы той области
совпадает с уравнением границы той области  , которая является далее областью интегрирования вплоскости
, которая является далее областью интегрирования вплоскости  .
.
Пример 3.3 Вычислим с помощью двойного интеграла объём тела, ограниченного поверхностями  и
и  .
.

Рисунок 3.5
Решение. Построим обе поверхности (правая часть конуса и цилиндр параболический) и тело, ограниченное ими (на рис. 3.5 оно выделено синим цветом). Чтобы составить двойной интеграл для вычисления объёма этого тела, необходимо построить цилиндр такой, чтобы выделенное тело было заключено в нём, и чтобы он проецировал тело на одну из координатных плоскостей в область  .
.
В данной задаче удобно спроецировать полученное тело на координатную плоскость  . (См. замечание 1)
. (См. замечание 1)
Исключим переменную y из системы уравнений, задающих тело:
 . Получим
. Получим  .
.
Это уравнение проецирующего цилиндра, а в плоскости  это уравнение окружности, ограничивающей область D1. (см. рис. 3.6).
это уравнение окружности, ограничивающей область D1. (см. рис. 3.6).
 Используя формулу (3.2), составим интеграл для вычисления объёма
Используя формулу (3.2), составим интеграл для вычисления объёма
 , где
, где  .
.
| Рисунок 3.6 |
 .
.
С учётом формы области D1 этот интегралвычислим в полярных координатах, введя их следующим образом:  .
.
Имеем:  .
.
Date: 2015-10-19; view: 900; Нарушение авторских прав