
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства тройного интеграла. Свойства тройных интегралов аналогичны свойствам двойных интегралов от функций, непрерывных в рассматриваемых областях
|
|
Свойства тройных интегралов аналогичны свойствам двойных интегралов от функций, непрерывных в рассматриваемых областях.
1. Линейность. Если функции интегрируемы по области  , то и их линейная комбинация интегрируема.
, то и их линейная комбинация интегрируема.

2. Аддитивность. Если область V разбита на две области V1 и V2, не имеющие общих точек, то

Примечание. Свойства 1 и 2 верны для любого фиксированного числа слагаемых.
3.Сохранение знака. Если в области V 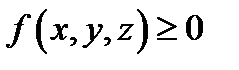 , то
, то  .
.
4. Интегрирование неравенств. Если в области V 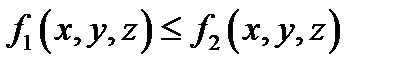 ,
,
то  ,
,
5. Для знакопеременной функции f(x,y,z) справедливо неравенство:
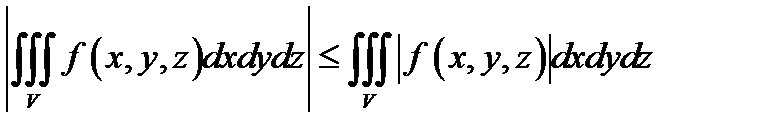 .
.
6. Интеграл от единичной функции по области  равен объёму этой области.
равен объёму этой области.
 (5.2)
(5.2)
7. Теорема об оценке. Если функция интегрируема по области  и в этой области
и в этой области  , то
, то  , где
, где  -объём области
-объём области  .
.
8.Теорема о среднем. Если функция f(x,y,z) непрерывна в замкнутой области V, то в этой области существует точка  , такая, что
, такая, что
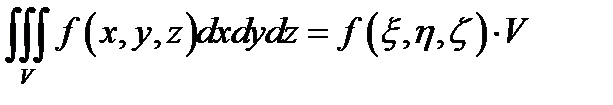 ,
,
где V – объем данной области.
4.Вычисление тройного интеграла.
Пусть замкнутая ограниченная область  проецируется на координатную
проецируется на координатную
плоскость  в правильную область
в правильную область  и любая прямая, перпендикулярная этой области
и любая прямая, перпендикулярная этой области  , пересекает граничную поверхность области
, пересекает граничную поверхность области  в двух точках (одна нижняя и одна верхняя).
в двух точках (одна нижняя и одна верхняя).
Т.е.  , где
, где 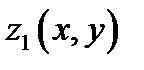 и
и  непрерывные функции в области
непрерывные функции в области  . Такая область
. Такая область  называется правильной.
называется правильной.
Теорема. Если  - правильная область с кусочно-гладкой границей,
- правильная область с кусочно-гладкой границей,  - непрерывная функция, то тройной интеграл
- непрерывная функция, то тройной интеграл  .
.
Если область  является y- правильной, то двойной интеграл в свою очередь сводится к повторному и
является y- правильной, то двойной интеграл в свою очередь сводится к повторному и
 . (5.3)
. (5.3)
В тройном интеграле, так же, как в двойном можно менять порядок интегрирования.
Пример 5.1 (2240) Расставим пределы интегрирования в тройном интеграле,  , где V – тетраэдр, ограниченный плоскостями
, где V – тетраэдр, ограниченный плоскостями 
Решение. Построим данные в условии плоскости и выделим тетраэдр, объём которого требуется вычислить (см. рис. (5.2)).
 Построенный тетраэдр проецируется в правильную область
Построенный тетраэдр проецируется в правильную область  , расположенную в плоскости
, расположенную в плоскости  , и любая прямая, проходящая через внутреннюю точку
, и любая прямая, проходящая через внутреннюю точку  перпендикулярно этой области, пересекает граничные поверхности тетраэдра в двух точках, в одной нижней и одной верхней. Т.е. тетраэдр занимает в пространстве правильную область
перпендикулярно этой области, пересекает граничные поверхности тетраэдра в двух точках, в одной нижней и одной верхней. Т.е. тетраэдр занимает в пространстве правильную область  .
.
| Рисунок 5. 2 |

| Рисунок 5.3 |
При этом  . Область
. Область 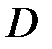 является
является  -правильной. Для всех её точек
-правильной. Для всех её точек  . Переходя к повторному интегралу, расставляем пределы интегрирования.
. Переходя к повторному интегралу, расставляем пределы интегрирования.
 .
.
Самостоятельно измените порядок интегрирования, спроецировав тетраэдр в другую координатную плоскость.
Пример 5.2 Вычислим объём тела, ограниченного поверхностями: 
 Решение. Построим заданные поверхности и выделим тело, объём которого требуется вычислить. (См. рис.5.3) Полученное тело проецируем в плоскость
Решение. Построим заданные поверхности и выделим тело, объём которого требуется вычислить. (См. рис.5.3) Полученное тело проецируем в плоскость  и получаем область
и получаем область  - сегмент круга.
- сегмент круга.
Определим границы сектора. Плоскость  пересекает параболоид по окружности, которая проецируется в часть границы области
пересекает параболоид по окружности, которая проецируется в часть границы области  :
:
| Рисунок 5. 3 |
 . Область
. Область  , занимаемая в пространстве телом
, занимаемая в пространстве телом  , является правильной и
, является правильной и 
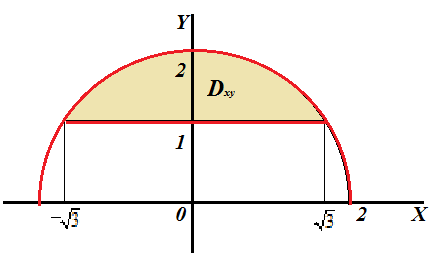
| Рисунок 5.4 |
 на отдельном рисунке 5.4. Заметим, что область и само тело являются симметричными относительно плоскости
на отдельном рисунке 5.4. Заметим, что область и само тело являются симметричными относительно плоскости 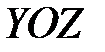 . Рассматривая область
. Рассматривая область  как x - правильную, с учётом симметрии, расставим пределы в повторном интеграле:
как x - правильную, с учётом симметрии, расставим пределы в повторном интеграле: 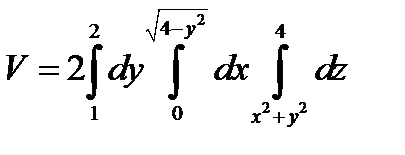 .
.
Ниже приведено подробное вычисление данного интеграла.



Домашняя работа к занятию 5:
ОЛ-6 №№ 2241, 2243, 2224, 2250, 2251 или ОЛ-5 №№ 8.109, 113, 115, 118, 120.
Date: 2015-10-19; view: 800; Нарушение авторских прав