Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Переход от двойного интеграла к повторному. Расстановка пределов интегрирования
|
|
| Рисунок 1.4 |
Для вычисления значения двойного интеграла (1.1) необходимо перейти к повторному интегралу вида (1.4а) или (1.4б). Способ перехода зависит от вида области D.
Область, ограниченная слева и справа прямыми
и 
,
а сверху и снизу - кривыми 
и 
, такими, что любая прямая 
, проведённая через область D, пересекает каждую из кривых и в одной точке, называется
y-правильной. При этом точку А называют точкой входа в область, а точку В – точкой выхода из области.
(см.рис 1.4) То есть область 
является y-правильной, если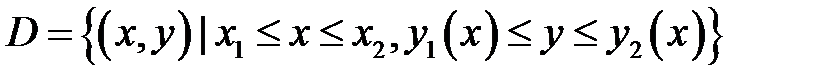 
Определив пределы изменения переменных по области D, расставляем пределы интегрирования в повторном интеграле:
. (1.4а)
| Рисунок 1.5 |
В этом случае имеем 
и
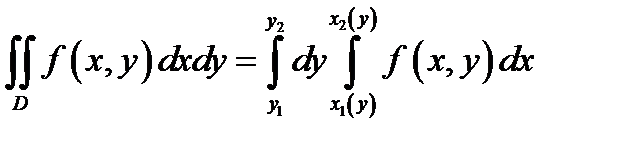(1.4б)
Пример 1.3. Расставить двумя способами пределы интегирования в двойном интеграле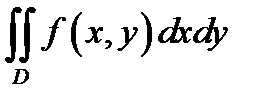 
, где D – треугольник с вершинами O(0,0), A(0,1),В(1,1).
Решение. Построим область D. Она одновременно является как
y-правильной, так и x-правильной. Поэтому первый способ расстановки пределов при переходе к повторному интегралу выглядит следующим образом:
для всех точек данной области переменная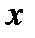 
изменяется между 
и 
, а переменная 
для любого из этих 
меняется от 
до 
, т.е..
Рис. 1.6
. Определив пределы изменения переменных по области D, расставляем пределы интегрирования в повторном интеграле:
. (См.(1.4а))
Изменим порядок интегрирования, то есть расставим пределы интегрирования в повторном интеграле вторым способом (См.(1.4б)).
Из рис. 1.6 следует, что для всех точек данной области переменная 
изменяется между 
и 
, а переменная 
для любого из этих 
меняется от 
до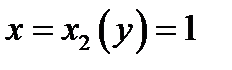 
. Т.е. 
Теперь расставляем пределы интегрирования:
.
Пример 1.4. Изменить порядок интегрирования в повторном интеграле 
.
Решение. Из данного интеграла следует, что область интегрирования ограничена прямыми 
, 
и кривыми 
, 
. 
Построим область D (См. рис. 1.7). Она является y-правильной, но не является x-правильной (См. рис.1.4). Для получения x-правильных областей придётся разбить область D на три части. Определим пределы, в которых меняются переменные по каждой из трёх областей для повторных интегралов вида (1.4б).
,
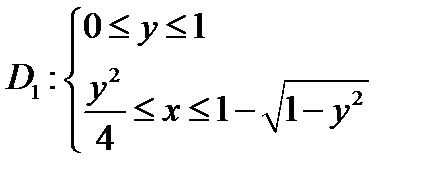По свойству аддитивности имеем
. Переходя к повторным интегралам вида (1.4б), расставляем пределы интегрирования в каждом из трёх слагаемых и получаем ответ:
.
Пример 1.5. Вычислим 
, где область 
ограничена лини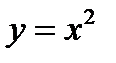й 
и 
.
Решение.
Линии, задающие область 
, пересекаются в точках с абсциссами 
| Рис. 1.8 |
и 
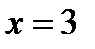. Построим область и выясним, является ли она правильной (См. рис.1.8). Сравнив данную область с областями, представленными на рис. 1.3 и рис. 1.4, видим, что наша область является y-правильной, но не является x –правильной.
Перейдём от двойного интеграла к повторному вида (1.4а) и вычислим его.
Учтём, что по области D переменные меняются в следующих пределах:
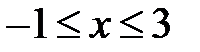и 
.
Расставим пределы интегрирования и вычислим интеграл. 
Date: 2015-10-19; view: 7561; Нарушение авторских прав