Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Момент инерции пластины относительно начала координат. вычисляется по формуле:
|
|
вычисляется по формуле:
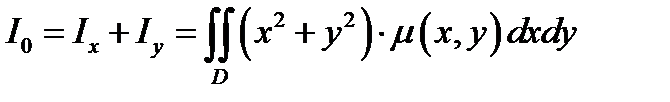(4.5)
Пример 4.1. (2225) Найти массу круглой пластинки радиуса R, если плотность в каждой точке пропорциональна расстоянию от центра и равна δ на краю пластинки.
Решение.
| Рисунок 4.2 |
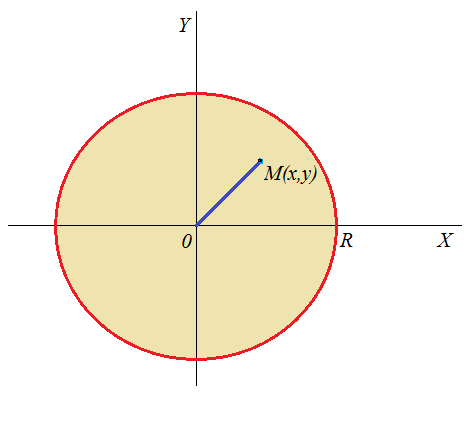Из условия следует, что если 
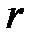- расстояние от центра до точки, а 
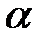- коэффициент пропорциональности, то плотность 
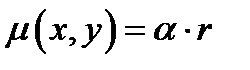. При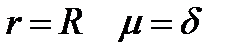 
. Следовательно, 
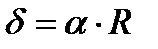, откуда получаем 
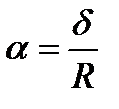. Искомую массу вычисляем по формуле (4.1), подставляя в неё найденную плотность.
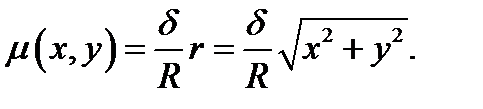
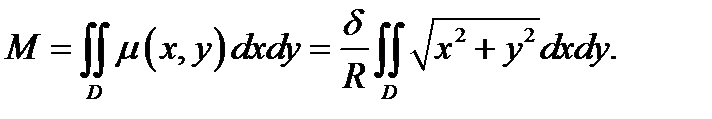
Расставим пределы интегрирования в повторном интеграле, переходя к полярной системе координат, и вычислим его:
.
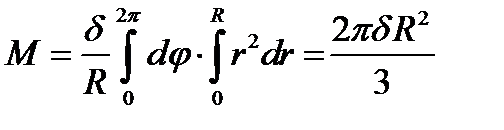Пример 4.2 (2237)
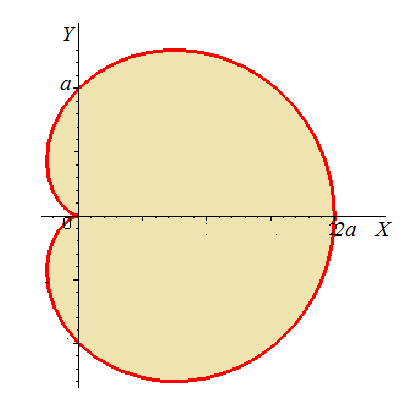
Найдём момент инерции относительно полюса фигуры, ограниченной кардиоидой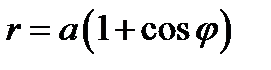 
, если плотность в каждой точке равна единице.
Решение.
Построим кардиоиду. (См. рис 4.3)
Момент инерции относительно полюса вычислим по формуле (4.5):
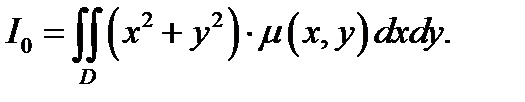
При расстановке пределов интегрирования в повторном интеграле перейдём к полярным координатам и затем вычислим интеграл. Получим
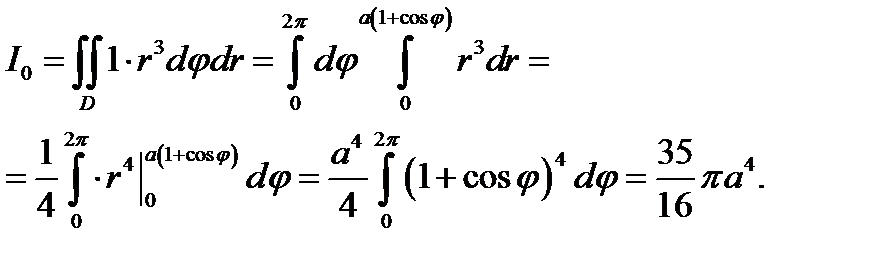
| Рисунок 4.3 |
Пример 4.3. Найдём координаты центра масс однородной пластинки, ограниченной частью эллипса и осями координат так, что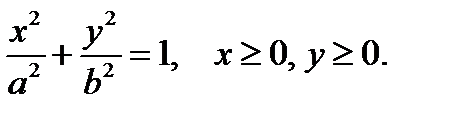 
Решение. Для удобства вычислений перейдём к обобщённым полярным координатам. Для эллипса они имеют вид: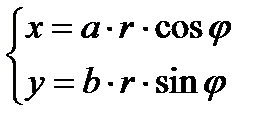 
, 
.
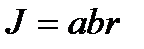Действительно, при подстановке в уравнение эллипса, имеем:
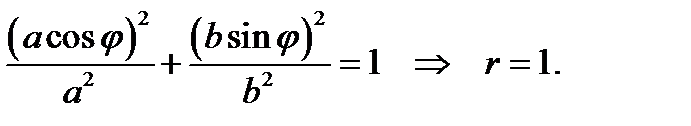Таким образом, четверть эллипса отображается в четверть единичной окружности.
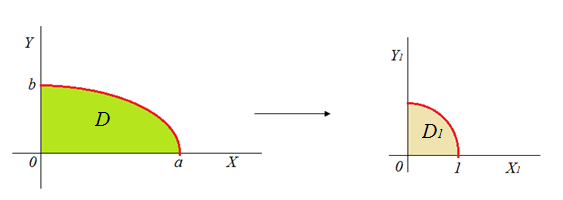
Рисунок 4.5
Далее, по формулам (4.1)- (4.3) вычисляем массу пластины, статические моменты и координаты центра масс. Плотность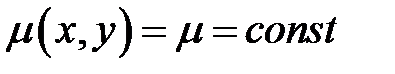 
Масса пластинки:
.
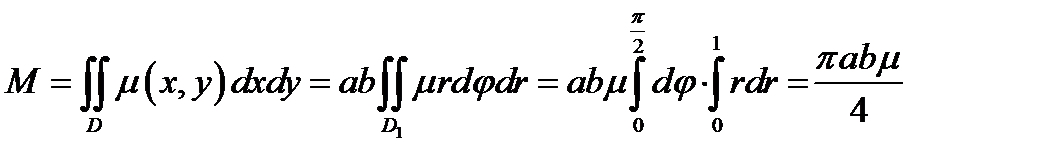Координаты центра масс:
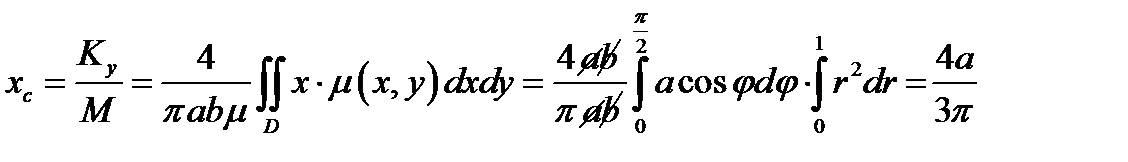
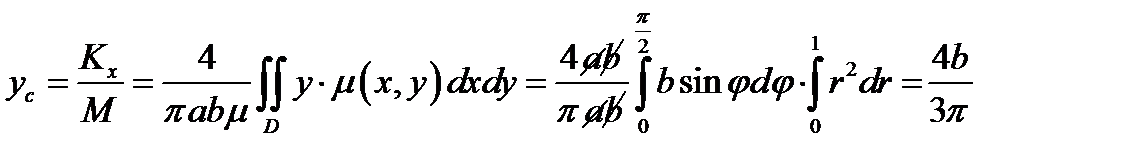. Ответ: 
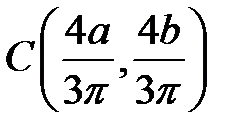. Домашнее задание к занятию 4:
ОЛ-6 №№ 2226, 2229, 2232, 2238 или ОЛ-5 №№ 8.93, 95, 100, 101, 105.
Занятие 5.
Тройной интеграл. Определение тройного интеграла и его свойства. Формулировка теоремы существования тройного интеграла. Сведение тройного интеграла к повторному и его вычисление в декартовой системе координат.
Ауд.: ОЛ-6 №№ 2240, 2242, 2245, 2248, 2249, 2253 или ОЛ-5 №№8.108, 111, 112, 116, 119
Date: 2015-10-19; view: 3585; Нарушение авторских прав