Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Композиция функций и взаимно обратные функции. 1 page
|
|
Определение: Пусть g функция из A в B, а f - функция из B в C. Тогда функция f(g), ставящая в соответствие каждому элементу xÎA элемент f(g(x))ÎC, называется композицией функций g и f и обозначается y = f(g(x)) (такую функцию называют также «сложной» функцией). Для композиции функций иногда используется обозначение g ◦ f.
Пример:
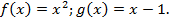
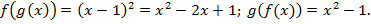
Определение: Функции f: A®B и g: B®A называются взаимно обратными, если для любого xÎA g(f(x) = x и для любого xÎB f(g(x)) = x. Заметим, что здесь обязательными являются условия: D(f) = E(g) и D(g) = E(f).
Графики взаимно обратных функций симметричны относительно прямой y = x (биссектрисы I и III координатных четвертей).
Пример:

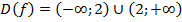 ,
, 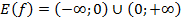 ;
;
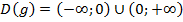 ,
, 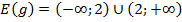 ;
;
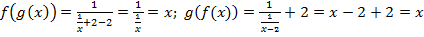 .
.
Таким образом, D(f) = E(g), D(g) = E(f), g(f(x))= f(g(x)) = x, следовательно, данные функции являются взаимно обратными.
|
1 уровень
53. Найдите область определения функции:
а) 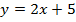 ; б)
; б)  ; в)
; в) 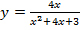 ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
54. Найдите область определения функции:
а) 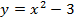 ; б)
; б) 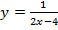 ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
55. Найдите область значений функций:
а) 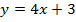 ; б)
; б) 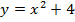 ; в)
; в)  ; г)
; г) 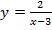 .
.
56. Найдите область значений функций:
а) 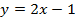 ; б)
; б) 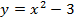 ; в)
; в) 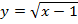 ; г)
; г) 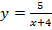 .
.
57. Докажите, что функция является четной:
а) 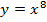 ; б)
; б) 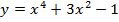 ; в)
; в)  ;
;
г) 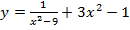 ; д)
; д)  ; е)
; е) 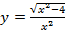 .
.
58. Докажите, что функция является четной:
а)  ; б)
; б) 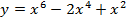 ; в)
; в) 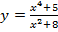 ;
;
г)  ; д)
; д) 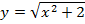 ; е)
; е)  .
.
59. Докажите, что функция является нечетной:
а)  ; б)
; б)  ; в)
; в) 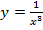 ;
;
г) 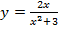 ; д)
; д) 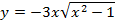 ; е)
; е) 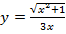 .
.
60. Докажите, что функция является нечетной:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 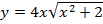 ; е)
; е) 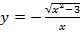 .
.
61. Найдите значение f(0), f(1), f(- 2):
а) 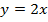 ; б)
; б) 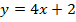 ; в)
; в) 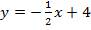 ; г)
; г) 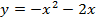 ;д)
;д) 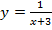 ;е)
;е) 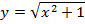 .
.
62. Найдите значение f(0), f(- 1), f(3):
а) 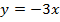 ;б)
;б) 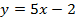 ;в)
;в) 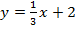 ;г)
;г)  ;д)
;д)  ;е)
;е)  .
.
63. Проведите общее исследование функции, заданной графиком:
а)
|
б)
|
64. Проведите общее исследование функции, заданной графиком:
| а) | б) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 уровень
65. Найдите значение функции в точке x0:
а)  ; б)
; б)  .
.
66. Найдите значение функции в точке x0:
а) 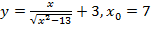 ; б)
; б) 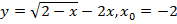 .
.
67. Найдите область определения функции:
а)  ; б)
; б)  .
.
68. Найдите область определения функции:
а)  ; б)
; б) 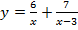 .
.
69. Найдите нули функции:
а)  ; б)
; б) 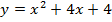 ; в)
; в)  ; г)
; г) 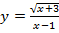 .
.
70. Найдите нули функции:
а)  ; б)
; б)  ; в)
; в) 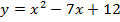 ; г)
; г) 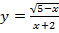 .
.
Date: 2015-10-18; view: 1064; Нарушение авторских прав