
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

III. Множество рациональных чисел Q
|
|
Q = 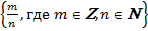 , то есть это множество всех дробей вида
, то есть это множество всех дробей вида 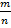 , где m - целое, n - натуральное.
, где m - целое, n - натуральное.
Очевидно, что множество рациональных чисел замкнуто относительно всех четырех арифметических операций, кроме деления на нуль.
Для рациональных чисел справедливо следующее утверждение.
Всякое рациональное число можно представить (записать) в виде конечной или бесконечной периодической десятичной дроби. Верно и обратное утверждение.
Примеры: 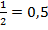 - конечная десятичная дробь;
- конечная десятичная дробь; 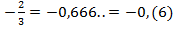 ;
;  – бесконечная периодическая дробь;
– бесконечная периодическая дробь; 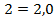 .
.
Множество рациональных чисел обладает замечательным свойством: оно всюду плотно, то есть между любыми двумя рациональными числами существует бесконечно много рациональных чисел. Поразительно, что, несмотря на это, если на числовой оси поставить все рациональные числа (допустим, что это возможно), то на числовой оси останется еще много свободных мест. И эти места занимают другие числа – иррациональные. (В середине I тысячелетия до нашей эры, предположительно, в школе Пифагора была открыта несоизмеримость отрезков: невозможно выразить рациональным числом диагональ квадрата со стороной, равной единице (это будет бесконечная непериодическая дробь  ) Это открытие стало причиной первого кризиса в математике, который был вскоре преодолен).
) Это открытие стало причиной первого кризиса в математике, который был вскоре преодолен).
IV. Множество иррациональных чисел J(J =  дополнение к множеству рациональных чисел Q).
дополнение к множеству рациональных чисел Q).
Это множество всех бесконечных непериодических дробей.
Примеры:  ;
; 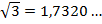 ;
; 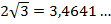
Данное множество существенно отличается от всех предыдущих тем, что оно незамкнуто относительно всех арифметических операций. (Убедитесь в этом, приведя соответствующие контрпримеры).
Заметим, что уравнение вида (3) 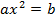 (при
(при  ), неразрешимое на множестве Q, на множестве иррациональных чисел имеет два решения
), неразрешимое на множестве Q, на множестве иррациональных чисел имеет два решения 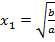 и
и 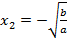 , то есть разрешимо.
, то есть разрешимо.
Большую роль играют два иррациональных числа, обозначаемых буквами
p = 3,1415926…»3,14
e = 2,718281828…»2,7
Числом p («пи») называется отношение длины окружности к ее диаметру. С числом e вы познакомитесь чуть позже…
Объединением множеств рациональных и иррациональных чисел является множество действительных (вещественных) чисел.
Date: 2015-10-18; view: 1795; Нарушение авторских прав