Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

VI. Множество комплексных чисел C
|
|

Любое комплексное число состоит из двух частей: действительной (a = Re z) и мнимой (b = Im z). Число i, с помощью которого расширяется множество R, называется мнимой единицей и определяется как число, квадрат которого равен -1.
Все ранее перечисленные числовые множества являются подмножествами множества C комплексных чисел.

|
|
Таким образом, что любое известное нам число является комплексным.
Примеры: 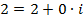 ;
;  ;
;  ;
; 
Действия с комплексными числами производятся по тем же правилам, что и с действительными числами.
Пример 1.
 ;
;
Пример 2.
 .
.
Комплексные числа изображаются точками координатной плоскости. Вводятся следующие понятия.
Пусть  некоторое комплексное число, тогда
некоторое комплексное число, тогда
1) 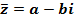 – число, сопряженное числу z. Заметим, что
– число, сопряженное числу z. Заметим, что  ;
;
2)  – модуль комплексного числа.
– модуль комплексного числа.
3) arg z = φ – аргумент комплексного числа z ≠ 0, угол между положительным направлением действительной оси и вектором, соответствующим числу z, причем угол считается положительным, если отсчет ведется против часовой стрелки, и отрицательным, отсчет ведется по часовой стрелке.
Заметим, что главные значения аргумента комплексного числа лежат на промежутке – π < arg z ≤ π.
Запись комплексного числа z в виде  называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Действительная и мнимая части комплексного числа z =  выражаются через его модуль
выражаются через его модуль  = r и аргумент φ следующим образом:
= r и аргумент φ следующим образом:  . Тогда комплексное число z можно записать в виде z = r(cos φ+i sin φ). Запись комплексного числа в таком виде называется тригонометрической формой записи.
. Тогда комплексное число z можно записать в виде z = r(cos φ+i sin φ). Запись комплексного числа в таком виде называется тригонометрической формой записи.
Пример: Записать число z = 1 - i в тригонометрической форме.
Найдем модуль данного числа:
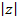 = r =
= r =  =
=  =
=  .
.
Аргумент φ находим, решая систему 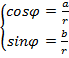 , т.е.
, т.е.  .
.
Таким образом φ =  , а данное комплексное число в тригонометрической форме имеет вид z = 1 – i =
, а данное комплексное число в тригонометрической форме имеет вид z = 1 – i =  .
.
На множестве С любое квадратное уравнение имеет два корня.
Пример: Решить уравнение  на множестве комплексных чисел.
на множестве комплексных чисел.




 или
или 
 или
или  .
.
Таким образом, уравнение  на множестве C имеет ровно два различных комплексных корня
на множестве C имеет ровно два различных комплексных корня  .
.
|
1 уровень
9. На отрезке [0; 3] укажите два натуральных, два целых, два рациональных и два иррациональных числа.
10. На отрезке [2; 4] укажите два натуральных, два целых, два рациональных и два иррациональных числа.
11. Рациональным или иррациональным числом будет длина диагонали прямоугольника со сторонами 1 и 5?
12. Рациональным или иррациональным числом будет длина гипотенузы прямоугольного треугольника с катетами 24 и 7?
13. Укажите, какие из следующих чисел являются иррациональными:  .
.
14. Укажите, какие из следующих чисел являются иррациональными:  .
.
15. Запишите рациональные числа в стандартном виде:
а) 1268,13; б) – 43,1109; в) 0,004204; г) - 0,392; д) 0,000902; е) 233129; ж) 14,321.
16. Запишите рациональные числа в стандартном виде:
а) 345,7; б) – 29,1293; в) 0,00043; г) - 0,496; д) 0,0075; е) 44457; ж) 17,358.
17. Запишите в виде десятичной дроби:
а) 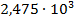 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
18. Запишите в виде десятичной дроби:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
19. Представьте обыкновенные дроби в виде десятичных периодических:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
20. Представьте обыкновенные дроби в виде десятичных периодических:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
21. Представьте периодические дроби в виде обыкновенных:
а) 0,(72); б) 0,(918); в) 0,(7263); г) 0,3(6) д) 0,11(6); е) 0,0(01).
22. Представьте периодические дроби в виде обыкновенных:
а) 0,(42); б) 0,(513); в) 0,(3584); г) 0,0(27) д) 0,2(35); е) 0,0(001).
23. Определите действительную (Re z) и мнимую (Im z) части комплексных чисел:
а) z = 1 + 3i; б) z = - 1 + 4i; в) z = - 6 - 5i; г) z =7 - i; д) z = 5i; е) z = 8.
24. Определите действительную (Re z) и мнимую (Im z) части комплексных чисел:
а) z = 6 + 2i; б) z = - 5 + 3i; в) z = - 3 - 8i; г) z = 6 - 3i; д) z = - 3i; е) z = - 5.
25. Найдите сопряженное ( ) и противоположное (- z) числа для комплексных чисел:
) и противоположное (- z) числа для комплексных чисел:
а) z =1 + 3i; б) z = - 1 + 4i; в) z = - 6 - 5i; г) z =7 - i; д) z = 5i; е) z = 8.
26. Найдите сопряженное ( ) и противоположное (- z) числа для комплексных чисел:
) и противоположное (- z) числа для комплексных чисел:
а) z = 6 + 2i; б) z = - 5 + 3i; в) z = - 3 - 8i; г) z = 6 - 3i; д) z = - 3i; е) z = - 5.
27. Вычислите:
а)  ; б)
; б) 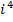 ; в)
; в)  ; г)
; г) 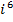 ; д)
; д)  ; е)
; е)  .
.
28. Вычислите:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
29. Найдите действительные числа x и y из уравнений:
а) (x – 8i) + (y - 3)i =1; б) (2x + y) + (x + 3y)i = 3 - i;
в) 2x – 5i + 7y + 2xi = - 7 - 5i; г) (3 + i)x – 2(1 + 4y) = 2 - i.
30. Найдите действительные числа x и y из уравнений:
а) (x + 2i) - (y + 2)i =3; б) (6x + y) + (3x - 4y)i = 8 - 5i;
в) 2x – 5yi – y + 3xi = 1 - 2i; г) (5 + i)x – 3(2 + 4y) = 6 + i.
31. Найдите сумму, разность и произведение комплексных чисел:
а) z1 = - 3 - 5i, z2 = 4 - 7i; б) z1 = 3,6 + 0,2i, z2 = 1,4 – 0,2i;
в) z1 = - 1 + 3i, z2 = 4 + 5i; г) z1 = 1,5 – 2,1i, z2 = 0,5 + 0,9i.
32. Найдите сумму, разность и произведение комплексных чисел:
а) z1 = 4 - 2i, z2 = 3 + 8i; б) z1 = - 0,6 + 0,2i, z2 = - 0,4 – 0,5i;
в) z1 = 3 – 0,7i, z2 = - 3 + 0,7i; г) z1 = - 1 + 6i, z2 = 6 - i.
33. Решите уравнения:
а) x2 + 25 = 0; б) x2 + 4 = 0;
в) x3 + 27 = 0; г) x3 – 27 = 0.
34. Решите уравнения:
а) x2 + 9 = 0; б) x2 + 16 = 0;
в) x3 + 8 = 0; г) x3 – 8 = 0.
2 уровень
35. Найдите значение выражений:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 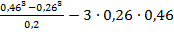 .
.
36. Найдите значение выражений:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
37. Докажите рациональность чисел:
а)  ; б)
; б)  .
.
38. Докажите рациональность чисел:
а)  ; б)
; б)  .
.
39. Выполните действия:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 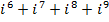 .
.
40. Выполните действия:
а) 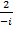 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 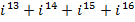 .
.
41. Решите уравнения:
а) (i – z)(1 + 2i) + (1- iz)(3 - 4i) =1+7i; б)  ;
;
в)  ; г)
; г)  .
.
42. Решите уравнения:
а) (2 i + z)(3 - i) + (4 + iz)(1 - 2i) = 11+3i; б)  ;
;
в)  ; г)
; г)  .
.
43. Найдите модуль и главное значение аргумента для каждого из заданных комплексных чисел. Записать эти числа в тригонометрической форме и изобразить их точками на плоскости:
а) z =  ; б) z = - 2i; в) z = 10; г) z = - 1 – i; д)
; б) z = - 2i; в) z = 10; г) z = - 1 – i; д)  .
.
44. Найдите модуль и главное значение аргумента для каждого из заданных комплексных чисел. Записать эти числа в тригонометрической форме и изобразить их точками на плоскости:
а) z = - 2 +2i; б) z = 5i; в) z = -7; г) z = 1 – i; д)  .
.
3 уровень
45. Вычислите:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
46. Вычислите:
а) 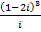 ; б)
; б)  ; в)
; в) 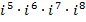 ; г)
; г)  ; д)
; д)  ; е)
; е) 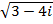 .
.
47. Изобразите множество точек, для которых выполняется заданное условие:
а) Re z = - 2; б) – 1 < Re z £ 3; в) – 1 £ Im z < 3; г)  ;
;
д) | z | < 2; е) | z + i | = 5; ж) 1 £ | z + 1 | < 2,5; з) | z +3 i | = | z - 3 |.
48. Изобразите множество точек, для которых выполняется заданное условие:
а) Re z = 3; б) – 2 £ Re z < 3; в) – 5 < Im z £ 6; г)  ;
;
д) | z | > 3; е) | z -2 i | = 3; ж) 1 < | z + 1 | £ 3; з) | z + 5i | = | z + 5 |.
49. Решите уравнения на множестве комплексных чисел:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
50. Решите уравнения на множестве комплексных чисел:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
51. Решите системы уравнений на множестве комплексных чисел:
а)  ; б)
; б)  .
.
52. Решите системы уравнений на множестве комплексных чисел:
а)  ; б)
; б)  .
.
 |
Date: 2015-10-18; view: 2170; Нарушение авторских прав