IV. Периодичность функции

Определение: Функция y = f(x) называется периодической, если существует число t ¹ 0, такое что для любого выполняются два условия:

1) ;

2) .

Обычно работают с наименьшим положительным значением t, называя его основным периодом и обозначая через Т; Т > 0.

График периодической функции состоит из повторяющихся с шагом Т фрагментов.

Примеры:

– периодическая, t = 2p n, n Î Z \{0}, Т = 2p;

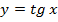– периодическая, t = p n, n Î Z \{0}, Т = p;

– периодическая, t = n, n Î Z \{0}, Т = 1 ( -дробная часть числа).

y

y= { x }

-1

x

V. Монотонность функции.

Определение: Функция y = f(x) называется возрастающей (убывающей) на некотором промежутке из области определения, если для любых точек x₁, x ₂ из этого промежутка из того, что x₁ < x ₂, следует, что f(x₁) < f(x₂) (f(x₁) > f(x₂)).

Говорят, что функция возрастает на промежутке J, если большему значению аргумента соответствует большее значение функции, и убывает, если большему значению аргумента из J соответствует меньшее значение функции.

Определение: Функция называется постоянной (const), если при любом допустимом значении аргумента она принимает одно и то же значение.

Графиком постоянной функции является прямая, параллельная оси абсцисс или совпадающая с ней.

Примеры: y = 2 – постоянная; y = 2 x – возрастает на R; y = 2 x ² – возрастает на [0; + ∞).

y = 2 x 2

y = 2 x

y

y=2

x

VI. Стационарные и критические точки функции.

Определение: Стационарными точками функции y = f(x) называются внутренние точки её области определения, касательная к графику в которых параллельна оси Оx.

y                                                                   y= f(x)                                                         x1     x2                           x                                                                                     Пример:

x 1 и x 2 – стационарные точки функции y = f(x).

Определение: Критическими точками функции y = f(x) называются внутренние точки её области определения, касательная к графику функции в которых либо параллельна оси Оx, либо не существует.

VII. Точки экстремума и экстремумы функции.

Определение: Внутренняя точка x₀ области определения функции y = f(x) называется точкой максимума этой функции, если существует число e > 0 такое, что для любого xÎ(x₀ - e; x₀ +e) выполняется неравенство: f(x₀)³ f(x).

Определение: Внутренняя точка x₀ области определения функции y = f(x) называется точкой минимума этой функции, если существует число e > 0 такое, что для любого xÎ(x₀ - e; x₀ +e) выполняется неравенство: f(x₀)£ f(x).

Замечание: Точки максимума и точки минимума функции называются её точками экстремум а, а значения функции в них – экстремумами (соответственно, максимумами или минимумами).

y                                       y= f(x)                                                                                     x0                                   x                                                                                       Пример 1. x0 – является критической точкой, но не является стационарной (в ней нельзя провести касательную). Также она не является точкой экстремума.

y                                                                 y= f(x)                                                           x0                                   x                                                                                       Пример 2. x0 – не является критической точкой, так как не входит в D(y).

y                                                                 y= f(x)                                       x0                                                     x                                                                                       Пример 3. x0 – является критической точкой, но не является стационарной (в ней нельзя провести касательную). Также она является точкой минимума.

y                                                                     y= f(x)                                                                       a       b         x                                                                                       Пример 4. Все точки xÎ[a;b] являются критическими и стационарными.

VIII. Выпуклость и точки перегиба графика функции.

Определение: Промежуток области определения функции называется промежутком её выпуклости вверх, если касательная, проведенная к графику функции в любой точке этого промежутка, расположена над графиком функции.

Определение: Промежуток области определения функции называется промежутком её выпуклости вниз, если касательная, проведенная к графику функции в любой точке этого промежутка, расположена под графиком функции.

Определение: Внутренняя точка области определения функции является её точкой перегиба, если «при переходе» через эту точку меняется характер выпуклости функции.

Date: 2015-10-18; view: 600; Нарушение авторских прав