Матрица билинейной формы

Пусть f - билинейная функция на n -мерном пространстве

L=Lⁿ над полем P, e ={e₁, …,e_n} - произвольный базис в L. Для

любых x, yÎ L имеем 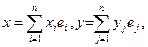где все x_i,y_jÎ P.

Тогда

f(x, y) = f 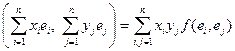. (24.1)

Формула (24.1) показывает, что функция f(x, y) является многочленом от координат х, у, все одночлены которого – первой степени по х и первой степени по у. Такой многочлен называется формой первой степени (то есть линейной) по х, и первой степени (то есть линейной) по у, то есть билинейной формой. Такие билинейные формы мы и будем изучать.

Очевидно, значение билинейной формы f(x,y) для произвольных x, yÎ L полностью и однозначно определяется n² значениями f(e_i,e_j) на упорядоченных парах базисных векторов e_i, e_j.

Определим квадратную матрицу 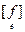= (f_ij) порядка n, где f_ij = f(e_i, e_j), i,j = 1,…,n. Матрица 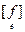называется матрицей билинейной формы f в базисе e.

Из формулы (24.1) f(x, y)= = = = = .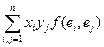

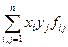Упражнение. Доказать обратное утверждение: если функция f задается формулой f(x, y)= 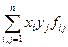, то f – билинейная функция, и матрица 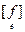= (f_ij).

Date: 2015-09-25; view: 389; Нарушение авторских прав