Эквивалентность билинейных форм и квадратичных форм

Пусть j: L® L - невырожденный линейный оператор, и g(x, y) - билинейная форма на пространстве L. Пусть по определению g^j(x, y)= g(j x,j y). Аналогично для квадратичной формы по определению G^j(x) = G(j x).

Упражнение. Проверить, что 1. g^j - билинейная форма,

2. (g^j )^y = g^{j y}, 3. g ^id = g, 4. если f = g^j , то g = .

Будем говорить, что билинейные формы f и g на пространстве L (соответственно, квадратичные формы F и G) находятся в отношении ~ (f ~ g, F ~ G), если существует невырожденный линейный оператор j: L® L такой, что f = g^j (соответственно, F = G^j).

Если j - унитарный оператор в Н^п (или ортогональный оператор в Е^п), то будем говорить, что формы f и g (F и G) находятся в отношении».

Упражнение. Проверить, что отношения ~ и» являются отношениями эквивалентности на множестве билинейных (соответственно, квадратичных) форм.

Определение. Формы f и g (соответственно, F и G) на-

зываются эквивалентными, если f ~ g (F ~ G).

Формы f и g (F и G) называются унитарно эквивалентными (ортогонально эквивалентными в случае Е^п), если f» g (F» G).

Так как g^j(x, y) = g(j x,j y) = [ j x ] ^t [ g ][ j y ] =

= [ x ] ^t [ j ] ^t [ g ][ j ][ y ] = [ x ] ^t( [ j ] ^t [ g ][ j ] ) [ y ] = [ x ] ^t [ g^j ][ y ], то

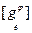= [ j ] ^t 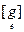[ j ] = 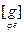= 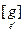, где е¢ = j е. Аналогично,

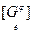= [ j ] ^t 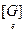[ j ] = = .

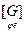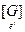Следовательно, f ~ g Û в произвольном базисе

[ f ] = T ^t [ g ] T, где T – некоторая невырожденная матрица. Так же f» g Û в произвольном ортонормированном базисе

[ f ] = T ^t [ g ] T, где T – некоторая унитарная (ортогональная

при L = Е^п) матрица. Очевидно, Т = [ j ]. Для квадратичных форм всё аналогично.

Следствие 1. f ~ g Û в L существуют базисы e и e¢ такие, что 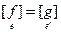. Соответственно, f» g Û в L - существуют ортонормированные базисы e и e¢ такие, что .

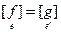Следствие 2. Если f ~ g, то rg f = rg g, то есть эквивалентные формы имеют равные ранги.

Действительно, rg f = rg 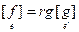= rg g.

Введенные нами отношения эквивалентности ~ и» разбивают множество билинейных (квадратичных) форм, определенных на пространстве L над P, на непересекающиеся классы эквивалентных форм. При изучении фактор-множества возникают важные вопросы: какой наиболее простой вид может иметь представитель каждого класса эквивалентных форм, сколько существует различных классов, какие формы эквивалентны, насколько выбором базиса в L можно упростить матрицу билинейной и квадратичной формы. Эти вопросы мы и будем далее рассматривать для квадратичных и симметричных билинейных форм.

Лекция 35.

Date: 2015-09-25; view: 821; Нарушение авторских прав