
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение. Свойства
|
|
Определение. Линейный оператор j: Н ® Н на унитарном пространстве Н называется унитарным, если
(j х, j у) = (х, у) " х, у Î Н.
Утверждение 1. Если j - унитарный оператор, то j - невырожденный.
Доказательство. Если хÎ Ker j, то (j х, j х) = (х, х) = 0 Þ х = 0 Þ Ker j = 0.
Утверждение 2. Если j - унитарный оператор, то
j -1 - унитарный оператор.
Доказательство. Пусть j -1х = а, j -1у = b. Тогда (а, b) = = (j a, j b) = (x, y) Þ (x, y)= (а, b) = (j -1х, j -1у).
Следовательно, унитарный оператор – это автоморфизм унитарного пространства Н (изоморфизм Н на себя).
Теорема 1. Для унитарного оператора j: Нn ® Нn эквивалентны следующие 14 условий:
1. (j х, j у) = (х, у) " х, у Î Нn.
2. (j еs, j et) = (еs, et) " s, t " (для некоторого) базиса
е = {е1,..,en} в Нn.
3. (j us ,j ut) = (us, ut) = dst " s, t " (для некоторого)
ортонормированного базиса и = {и1,..,иn} в Нn.
4. {j u1 ,…,j un } – ортонормированный базис.
5. 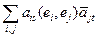 =
= 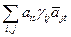 = gs,t, где gi,j = (еi, ej) –
= gs,t, где gi,j = (еi, ej) –
элементы матрицы Грама, а (ai,j) = [  ].
].
6.  = ds,t , где (bs,t) = [
= ds,t , где (bs,t) = [  ].
].
7. [  ] t
] t 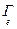
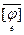 =
= 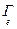 .
.
8. [  ] t
] t 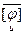 = Е и
= Е и 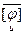 t [
t [  ] = Е.
] = Е.
9. [  ] -1 =
] -1 = 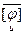 t.
t.
10. [  ]
] 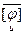 t = Е.
t = Е.
11.  = ds,t.
= ds,t.
12. Строки матрицы [  ] являются ортонормированным
] являются ортонормированным
базисом в C n.
13. Столбцы матрицы [  ] являются ортонормированным базисом в пространстве столбцов C п.
] являются ортонормированным базисом в пространстве столбцов C п.
14. [  ] t – матрица унитарного оператора.
] t – матрица унитарного оператора.
Доказательство теоремы аналогично доказательству теоремы 1 из п.19.1.
Упражнение. Доказать теорему 1.
Следствие. Если j - унитарный оператор, то |det j | = 1, то есть detj - комплексное число, у которого модуль равен 1.
Доказательство. Так как [  ]
] 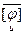 Т = Е, то detj×
Т = Е, то detj× 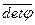 =
=
= detЕ = 1 Þ |det j | 2 = 1 Þ |det j | = 1.
Date: 2015-09-25; view: 393; Нарушение авторских прав