Определение квадратичной формы. Связь билинейных и квадратичных форм. Матрица и ранг квадратичной формы

Определение. Пусть f - билинейная функция на линейном пространстве L над P. Функция F: L ® P, заданная формулой F(x) = f(x, x) " x Î L, называется квадратичной функцией, определяемой билинейной функцией f.

Если f(x, y)= 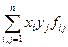, то F(x) = 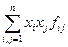- многочлен, все одночлены которого имеют вторую степень по координатам х, то есть это форма второй степени, или же квадратичная форма. Таким образом, квадратичная функция F(x) задается квадратичной формой от координат х.

Упражнение. Доказать, что соответствие f ® F не инъ-

ективно.

Определение. Билиненая форма (функция) f называется симметричной, если f(x, y) = f(y, x) " x, y Î L.

Упражнение. Доказать, что f – симметрична Û f(e_i, e_j) = = f(e_j, e_i) " i, j " (для некоторого) базиса e Û 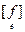= 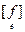^t.

Утверждение. Если char P ¹ 2, то соответствие f «F между симметричными билинейными и квадратичными формами является биекцией.

Доказательство. Пусть f - симметричная билинейная форма, и f ® F. Тогда " x, yÎ L F(x + y) = f(x + y, х + у)= = f(x, х) + f(y, у) + f(x, y)+ f(y, x) = F(x) + F(y) + 2 f(x, y) Þ

f(x, y)= 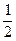(F(x + y) - F(x) - F(y)). (24.2)

Следовательно, билинейная форма f однозначно восстанавливается по определенной ею квадратичной форме F, и значит, соответствие f ® F является инъекцией.

Date: 2015-09-25; view: 383; Нарушение авторских прав