Доказательство. 1. Если F(x) = 0 x Î L, то из (24.2) f(x, y) = 0 x, у Þ

1. Если F(x) = 0 " x Î L, то из (24.2) f(x, y) = 0 " x, у Þ

любой базис в L является f- ортогональным.

2. Если же $ е Î L такой, что F(е) ¹ 0, то пусть е = е₁,

L₁ = <е₁>, L₂ = {xÎ L | f(е₁, x) = 0}. Легко проверить, что L₂ – подпространство. Будем называть L₂ ортогональным дополнением к L₁ в смысле формы f и обозначать 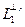. Докажем, что L = L₁ Å .

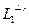a) Пусть хÎ L₁ 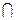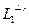. Тогда х= a е₁ Þ f(е₁,aе₁)=a f(е₁, е₁) = = a F(е₁) = 0 Þ a = 0 Þ x = 0 Þ L₁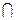 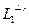= 0.

б) Покажем, что " х Î L $ a Î Р такое, что х = aе₁ + у, где у Î 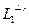. В самом деле, у Î 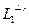Û (х - aе₁) ^ _f е₁ Û

f(х - aе₁, е₁) = 0 Û a = f(х, е₁)/ f(е₁, е₁) (так как f(е₁, е₁)= =F(е₁)¹ 0).

Таким образом, L = L₁ Å 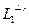, dim 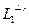= n – 1, и для 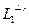можно считать, что утверждение теоремы выполнено по предположению индукции, то есть в 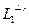$ f- ортогональный базис {е₂,е₃,…,е_n}. Тогда, очевидно, {е₁,е₂,…,е_n} - f- ортого- нальный базис в L.

ÿ

Итак, мы нашли базис e = {е₁,…,е_n} такой, что f(е_i, е_j) = 0 при i ¹ j. Пусть f(е_i, е_i) = l _i. Тогда в этом базисе

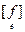= diag(l₁,…, l_n); f(x, y) = 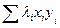, F(x) = 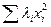, и такой вид билинейной и квадратичной форм называется каноническим. Следовательно, любая симметричная билинейная форма и любая квадратичная форма эквивалентны формам канонического вида. То есть существует линейная замена координат, которая приводит произвольную симметричную билинейную форму (квадратичную форму) к каноническому виду.

Пусть f(е_i, е_i) = l _i ¹ 0 при i = 1,…,r и f(е_i, е_i) = 0 при

i = r+1,…,п. Тогда r = rg f, и r от базиса не зависит.

Рассмотрим случай Р = С. Возьмём m_i Î С такие, что

m_i² = l _i при i = 1,…,r, m_i = 1 при i = r+1,…,п. Тогда после замены координат z_i = m_ix "i получим F(x)= z₁²+…+z_r² - такой вид квадратичной формы называется нормальным.

Итак, нами доказана

Теорема. В линейном пространстве над полем С для любой квадратичной формы F существует базис e¢ ={e₁¢,…,e_п¢}, в котором форма имеет нормальный вид, то есть для х=

F(x) = z₁²+…+z_r². Соответствующая симметричная билинейная форма имеет нормальный вид f = z₁ w₁+…+z_r w_r.

Следствие. Над полем С класс эквивалетных форм определяется рангом r. Формы с одинаковым рангом эквивалентны, формы с разными рангами не эквивалентны. Существует r+1 классов эквивалентных форм.

Теперь рассмотрим случай Р = R. Будем считать, что форма F имеет канонический вид F(x) = l₁х₁²+…+l_sx_s² –

- l_s+1х_s+1²-…- l_s+t х_s+t², где все l_i > 0, s+t = r. Пусть m_I = 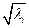при i = 1,…,r, m_i = 1 при i = r+1,…,п. Тогда после замены координат z_i= m_ix "i получим F(x)= z₁²+…+z_s²– z_s+1²-…-z_s+t² - такой вид квадратичной формы в случае поля R называется нормальным.

Таким образом, нами доказана

Теорема. В линейном пространстве L над полем R для любой квадратичной формы F существует базис, в котором форма имеет нормальный вид F(z) = z₁²+…+z_s²– z_s+1²-…-z_s+t². Соответствующая симметричная билинейная форма f имеет нормальный вид f(z, w) = z₁ w₁+…+z_s w_s – z_s+1w_s+1-…- z_s+tw_s+t.

Date: 2015-09-25; view: 372; Нарушение авторских прав