Закон инерции для квадратичных форм

Теорема (закон инерции). Если форма F в базисе е имеет нормальный вид F(z) = z₁²+…+z_s²– z_s+1²-…-z_s+t², то числа s и t от базиса не зависят, то есть для любого базиса е¢, в котором F имеет нормальный вид, числа s и t будут теми же самыми.

Доказательство. Докажем, что s равно максимальной размерности подпространства в L, на котором F > 0. Отсюда и будет следовать независимость s от базиса. Очевидно, если е = {е₁,е₂,…,е_n}, то подпространство L₁ = <е₁,е₂,…,е_s> такое, что > 0. Таким образом, существует подпространство размерности s, на котором F > 0.

Покажем, что не существует подпространства размерности большей s, на котором F > 0. Предположим противное: пусть L₂ – подпространство, на котором F > 0, и dimL₂ > s. Рассмотрим подпространство L₃ = <е_s+1,…,е_n>. Очевидно, 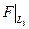£ 0. По теореме 3 из п.12 dimL₂ 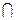L₃ = dimL₂ + dimL₃ – – dim(L₂+L₃) > s + (n – s) – n = 0 Þ если L₂ 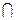L₃ ' х, х ¹ 0, то F(х)> 0 и F(х)£ 0 - противоречие, то есть L₂ не существует, и для s теорема доказана.

Далее рассмотрим форму – F. Теперь числа t и s меняются ролями, и t – это максимальная размерность подпространства в L, на котором – F > 0. То есть t также не зависит от базиса.

ÿ

Определение. Число s называется положительным индексом инерции формы F и обозначается I⁺(F). Число t называется отрицательным индексом инерции формы F и обозначается I ^-(F).

Из доказанной теоремы следует корректность определения индексов инерции.

Следствие. Квадратичные формы имеют 2 числовых инварианта I⁺ = s, I ^- = t, которые независимы и составляют полную систему инвариантов, так как определяют квадратичную форму с точностью до эквивалентности. Другими словами, любой класс эквивалентных квадратичных форм однозначно определяется парой чисел (s, t).

Упражнение. Посчитать количество классов эквивалентных форм.

Date: 2015-09-25; view: 377; Нарушение авторских прав