Сопряженное линейное пространство

Рассмотрим на Н^п функцию f_a(х) = (х, а), где а Î Н^п.

Упражнение. Проверить, что f_a Î (Н^п)*.

Рассмотрим отображение Ф: Н^п ® (Н^п)* такое, что для

а Î Н^п Ф(а) = f_a.

Очевидно, Ф(а+b) = f_a+b = Ф(а) + Ф(b) = f_a + f_b, так как f_a+b(х) = (x, а+b) = (х, а) + (x, b) = f_a(х) + f_b(х) = (f_a + f_b)(х). Ф(aа) = f_aa = 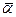Ф(а) = 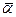f_a, так как f_aa(х)=(х, aа)= 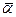(х, а)= = 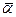(f_a(х)) = ( 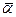f_a)(х).

Следовательно, Ф – не является линейным отображением. Будем называть такие отображения полулинейными.

Упражнение. Пусть вектор а в ортонормированном базисе и имеет координаты (a₁, а₂,…,а_п). Проверить, что в сопряженном базисе и* функция Ф(а) = f_a имеет координаты (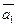, ,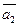…, 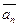). Следовательно, Ф – биекция.

Будем говорить, что Ф – полуизоморфизм пространств Н^п и (Н^п)*. Таким образом, нами доказано

Утверждение. Отображение Ф: Н^п ® (Н^п)* такое, что

для а Î Н^п Ф(а) = f_a является полуизоморфизмом линей-

ных пространств Н^п и (Н^п)*.

Замечание. Полуизоморфизм Ф является каноническим, то есть он не зависит от базиса.

Date: 2015-09-25; view: 322; Нарушение авторских прав