Определения, примеры. Определение. Линейное пространство H над полем C называется унитарным (или эрмитовым) пространством

Определение. Линейное пространство H над полем C называется унитарным (или эрмитовым) пространством, если на Н фиксирована функция двух векторных аргументов х, у Î Н со значениями в С, которая называется скалярным произведением, обозначается (х, у), и обладает свойствами

1. (х + у, z) = (х, z) + (у, z) " х, у, z Î Н,

2. (ax, y) = a (x, y) " х, у Î Н, " a Î С,

3. (x, y) = 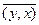" х, у Î Н (черта над числом означает комплексное сопряжение),

4. (x, x) > 0 " х Î Н, x ¹ 0.

Заметим, что из свойства 3 комплексное число (x, x) яв-

ляется действительным, так как (x, х) = 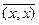, и неравенство в свойстве 4 имеет смысл.

Свойства 1, 2 означают линейность скалярного произведения по первому аргументу, свойство 3 называется эрмитовостью скалярного произведения, свойство 4 называется положительной определённостью.

Следствия из определения.

1. (х,у+z)= 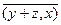= 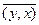+ 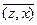= (х, у)+ (х, z) " х, у, zÎ Н.

2. (х, aу) = 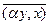= = 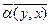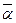(х, у) " х, у Î Н, " a Î С.

Следствие 1 означает, что для скалярного произведения выполняется одно из двух свойств линейности по второму аргументу. Следствие 2 показывает, что второе свойство линейности по второму аргументу не выполняется. Поэтому скалярное произведение в Н называют полуторалинейной эрмитовой положительно определенной функцией.

3. (0_Н, х) = (0 _С ×0_Н , x) = 0 _С ×(0_Н , x) = 0 _С Þ (0_Н , 0_Н) = 0 _C.

4. Пусть е = {е₁,…, е_n } – базис в Н, .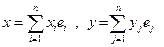

Тогда (x, y) = () = = ,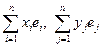

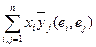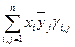где g_i,j = (e_i,е_j), а матрица Г = 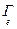= (g_i,j) называется матрицей Грама. Очевидно, (x,y)= 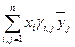= = [ 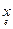] ^tГ 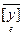, и Г ^t = . Черта над матрицей означает замену всех элементов матрицы на комплексно сопряженные.

Date: 2015-09-25; view: 345; Нарушение авторских прав