
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение. Свойства. Определение. Линейный оператор j : Е ® Е называется ортогональным, если (j х, j у) = (х, у) х
|
|
Определение. Линейный оператор j: Е ® Е называется ортогональным, если (j х, j у) = (х, у) " х, у Î Е.
Утверждение 1. Если j - ортогональный оператор, то j -
невырожденный.
Доказательство. Если хÎ Ker j, то (jх, jх) = (х, х) = 0 Þ х = 0 Þ Ker j = 0.
Утверждение 2. Если j - ортогональный оператор, то
j -1 - ортогональный оператор.
Доказательство. Пусть j -1х = а, j -1у = b. Тогда (а, b) = = (ja, jb) = (x, y) Þ (x, y)= (а, b) = (j -1х, j -1у).
Таким образом, ортогональный линейный оператор – это автоморфизм евклидова пространства Е (изоморфизм Е
на себя).
Теорема 1. Для ортогонального оператора j: Еn ® Еn эквивалентны следующие 15 условий:
1. (j х, j у) = (х, у) " х, у Î Еn.
2. (j х, j х) = (х, х) (то есть | jх | = | х |) " хÎ Еn.
3. (j еs, j et) = (еs, et) " s, t " (для некоторого) базиса
е = {е1,..,en} в Еn.
4. (j us ,j ut) = (us, ut) = dst " s, t " (для некоторого)
ортонормированного базиса и = {и1,..,иn} в Еn.
5. {j u1 ,…,j un } – ортонормированный базис.
6. 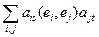 =
= 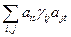 = gs,t, где gi,j = (еi, ej) –
= gs,t, где gi,j = (еi, ej) –
элементы матрицы Грама, а (ai,j) = [  ].
].
7.  = ds,t , где (bi,j) = [
= ds,t , где (bi,j) = [  ].
].
8. [  ] t
] t 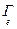 [
[  ] =
] = 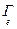 .
.
9. [  ] t [
] t [  ] = Е.
] = Е.
10. [  ] t = [
] t = [  ] -1.
] -1.
11. [  ][
][  ] t = Е.
] t = Е.
12. 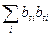 = ds,t.
= ds,t.
13. Строки матрицы [  ] являются ортонормированным
] являются ортонормированным
базисом в R n.
14. Столбцы матрицы [  ] являются ортонормированным
] являются ортонормированным
базисом в пространстве столбцов R п.
15. [  ] t – матрица ортогонального оператора.
] t – матрица ортогонального оператора.
Доказательство. Очевидно, из 1 Þ 2,3,4 (как частные
случаи), 6 Û 8, 7 Û 9 Û 10 Û 11 Û 12 Û 13 Û 15, 4 Û 5 Û 7 Û 14.
Из 2 Þ 1, так как 2(jх,jу)=(jх+jу,jх+jу) - (jх,jx) - (jy,jy)= = |j(х+у)|2 - | jх |2 - | jy |2 =| х+у |2 - | х |2 - | y |2 = 2(х, у).
Из 3 Þ 1, так как (jх, jу) = (j(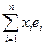 ), j(
), j( 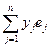 )) =
)) =
=  =
=  = (
= (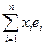 ,
, 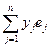 )= (х, у).
)= (х, у).
Так же проверяется, что из 4 Þ 1.
И наконец, 3 Û 6, так как (jеs, jet) = (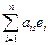 ,
, 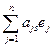 )=
)=
= 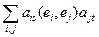 =
= 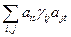 .
.
ÿ
Следствие. Если j - ортогональный оператор, то
det j = ±1.
Доказательство. [  ] t [
] t [  ] = Е Þ det ( [
] = Е Þ det ( [  ] t [
] t [  ] ) =
] ) =
= det [  ] t× det [
] t× det [  ] = (det [
] = (det [  ] )2 = det Е = 1.
] )2 = det Е = 1.
Определение. Матрица А называется ортогональной, если А - матрица некоторого ортогонального оператора в ортонормированном базисе, то есть, если для неё выполняется одно из эквивалентных условий Теоремы 1 под номерами 7, 9, 10, 11, 12, 13 или 14.
Date: 2015-09-25; view: 402; Нарушение авторских прав