Сопряженные линейные пространства

Пусть L =Lⁿ – линейное пространство над полем Р. Обозначим через L* множество линейных функций на L со значениями в Р (см. п.13.1, важный частный случай линейных отображений). Так как множество Ф(Lⁿ,L^m)={j: Lⁿ ® L^m} линейных отображе­ний из Lⁿ в L^m с операциями сложения и умножения на эле­менты поля является линейным пространством над полем P (см. п.13.5) и существует изоморфизм линейных пространств Ф(Lⁿ,L^m)» М_т,п(Р), то L*= Ф(Lⁿ, Р) - линейное пространство, и L*» М_1,п(Р)= Р ⁿÞ dimL*=n= dimL. В частности, L*» L, но этот изоморфизм не канонический – он зависит от выбора базисов в L и L*.

В качестве базисного вектора одномерного линейного пространства Р возьмем 1 _Р. Пусть е = {e₁,…,e_п} – базис пространства L, х = х₁e₁+…+х_пe_п , f Î L*. Тогда

f(x) = х₁f(e₁)+…+х_пf(e_n) = х₁a₁+…+х_пa_n, где все a_i Î P,

a_i = f(e_i) = a_i×1 _Р, и f « [ 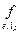] = (a₁,…,a_n)Î Р ⁿ. Базисным

строчкам (0,0,…,0, 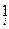,0,…,0) в Р ⁿ соответствуют в L* линейные функции еⁱ такие, что еⁱ(х)= 0×х₁+…+1×х_i+…+0×х_n= х_i. Очевидно, е *= {е¹,…,еⁿ} – базис в L*, и f = a₁е¹ +…+ a_пе^п.

Кроме того, еⁱ(е_j)= d ⁱ_j =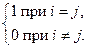

Определение. Линейное пространство L* называется

сопряженным (или двойственным, или дуальным) к простра-

нству L. Базис е * называется сопряженным (или двойственным, или дуальным) к базису е.

Пусть теперь L= Е^п, f_a(х)= (a, x).

Упражнение. Проверить, что f_a Î (Е^п)*.

Утверждение. Отображение Ф: Е^п ® (Е^п)* такое, что для а Î Е^п Ф(а) = f_a является изоморфизмом линейных пространств Е^п и (Е^п)*.

Доказательство. Проверим линейность отображения Ф. Ф(а+b)= f_a+b= Ф(а)+Ф(b) = f_a+ f_b, так как f_a+b(х)= (а+b, x) = = (а, x)+ (b, x) = f_a(х)+ f_b(х) =(f_a+ f_b)(х). Ф(aа)= f_aa= aФ(а)= = a f_a, так как f_aa(х) = (aа, х) = a(а, х) = a (f_a(х)) = (a f_a)(х). Найдем теперь KerФ. Пусть а Î KerФ Þ Ф(а) = f_a = 0 Þ f_a(х) = 0 " х Þ f_a(а) = (а, а) = 0 Þ а = 0 Þ KerФ = 0 Þ Ф – инъекция, сюръекция, биекция (см. теорему 6 из п.15) Þ Ф – изоморфизм.

ÿ

Date: 2015-09-25; view: 358; Нарушение авторских прав