
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сопряженные линейные операторы
|
|
Пусть j: Еп ® Еп - линейный оператор. Рассмотрим функцию f(x) = (a, j x).
Упражнение. Проверить, что f – линейная функция, то
есть f Î (Еп)*, и следовательно, f = fb при некотором bÎ Еп.
Будем считать, что b = j*a, где j*: Еп ® Еп - некоторое отображение. Из определения j* получаем, что
(a, j x) = (b, x) = (j*a, x) или (j x, а) = (х, j*a).
Утверждение. j*: Еп ® Еп – линейный оператор.
Доказательство. (х, j*(a+b)) = (j x, a+b) = (j x, a) +
+ (j x, b) = (х, j*a) + (х, j*b) = (х, j*a + j*b) Þ j*(a+b) =
= j*a+j*b (см. утверждение из п. 20.1). Аналогично,
(х, j*(aa)) = (j x, aa) = a(j x, a)= a (х, j*a) = (х, aj*a) Þ
j*(aa) = aj*a. ÿ
Определение. Линейный оператор j*: Еп ® Еп называется сопряженным к линейному оператору j.
Очевидно, j** = j, так как (j х, у) = (х, j*у) = (j**х, у).
Заметим, что при отождествлении Ф: а «fa получаем:
(a, j x) = (j*a, x), то есть fa(j x) = j*(fa)(x) Þ j*(fa)= fa◦j.
Теорема. Для линейных операторов j и y на Еп эквивалентны следующие 5 условий (и при выполнении любого из этих условий y = j*, j = y*):
1. (j x, у) = (х, yу) " х, у Î Еп.
2. (j еi,еj)= (еi,y еj) " i, j " (для некоторого) базиса е в Еп.
3. (j иi,иj)= (иi,y иj) " i, j " (для некоторого) ортонормированного базиса и в Еп.
4. [  ] t ×
] t × 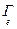 =
= 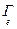 × [
× [ 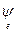 ], или же [
], или же [ 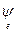 ] =
] = 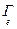 -1× [
-1× [  ] t ×
] t × 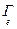 , где
, где 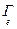 - матрица Грама для базиса е. (Доказать, что Г-1 $ - см. также п.24.3).
- матрица Грама для базиса е. (Доказать, что Г-1 $ - см. также п.24.3).
5. [  ] = [
] = [  ] t.
] t.
Доказательство. Очевидно, из 1 Þ 2 (как частный случай), из 2 Þ 1 ввиду линейности j и скалярного произведения. Аналогично, 1 Û 3. Проверим, что 2 Û 4. В самом деле, если [  ] = (аks), [
] = (аks), [ 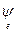 ] = (bks), то (j еi,еj) = (
] = (bks), то (j еi,еj) = (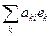 ,еj) = =
,еj) = = 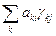 = ( [
= ( [  ] t ×
] t × 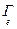 )ij – (i,j)- й элемент матрицы [
)ij – (i,j)- й элемент матрицы [  ] t ×
] t × 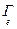 . А (еi,y еj)= (еi,
. А (еi,y еj)= (еi, 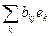 ) =
) = 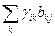 = (
= ( 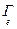 × [
× [ 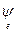 ] )ij – (i,j)- й элемент матрицы
] )ij – (i,j)- й элемент матрицы 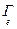 × [
× [ 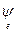 ]. Отсюда 2 Û 4. Аналогично проверяется, что 3 Û 5. ÿ
]. Отсюда 2 Û 4. Аналогично проверяется, что 3 Û 5. ÿ
Date: 2015-09-25; view: 409; Нарушение авторских прав