Доказательство. Þ. Пусть L1 + L2 = L1 Å L2

Þ. Пусть L₁ + L₂ = L₁ Å L₂. Тогда "хÎ L₁ + L₂ представление х = х₁ + х₂, х₁Î L₁, х₂ÎL₂, однозначно. И однозначным является выражение векторов х₁ , х₂ через базисы подпространств: х₁ = a₁е₁+…+a_kе_k, х₂ = a_k+1е_k+1+…+a_mе_m. Следовательно, и выражение х = a₁е₁+…+a_kе_k+a_k+1е_k+1+…+a_mе_m однозначно Þ {e₁ ,…,e_k,e_k+1 ,…,e_m} – базис подпространства L₁ + L₂.

Ü. Если {e₁ ,…,e_k,e_k+1 ,…,e_m} – базис подпространства L₁ + L₂, то "хÎL₁+ L₂ выражение х = a₁е₁+…+a_kе_k+a_k+1е_k+1+…+a_mе_m однозначно. Тогда и для х₁ = a₁е₁+…+a_kе_k Î L₁,

х₂ = a_k+1е_k+1+…+a_mе_mÎ L₂ представление х = х₁ + х₂ – однозначно, то есть L₁ + L₂ = L₁ Å L₂.

ÿ

Следствие. dim(L₁ Å L₂) = dim L₁ + dim L₂.

Упражнение. Доказать, что L₁+…+L_k = L₁ Å…Å L_k Û объединение базисов всех подпространств L_i является базисом подпространства L₁ +…+L_k.

Теорема 3. dim(L₁ + L₂) + dim(L₁ 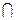L₂)= dimL₁ + dim L₂.

Доказательство. Пусть {e₁ ,…,e_d} – базис в L₁ 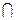L₂. Дополним его до базиса {e₁ ,…,e_d, f₁ ,…, f_k } подпространства L₁ и до базиса {e₁ ,…,e_d,g₁ ,…,g_m} подпространства L₂. Покажем, что {e₁ ,…,e_d, f₁ ,…, f_k, g₁ ,…,g_m} – базис подпространства L₁+ L₂. В самом деле, "хÎ L₁ + L₂, х = х₁ + х₂, х₁Î L₁, х₂ÎL₂, х₁Î <е₁,…,е_d, f₁,…, f_k >, х₂Î <е₁,…,е_d, g₁,…, g_m > Þ

х₁ + х₂Î <е₁,…,е_d, f₁,…, f_k, g₁,…, g_m >. Покажем, что система векторов {е₁,…,е_d, f₁,…, f_k, g₁,…, g_m } линейно независима. Пусть a₁е₁+…+a_dе_d +b₁f₁+…+b_kf_k +g₁g₁+…+g_mg_m = 0. Тогда a₁е₁+…+a_dе_d +b₁f₁+…+b_kf_k = -(g₁g₁+…+g_mg_m) Î L₁ 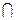L₂ Þ b₁=…=b_k = 0 Þ a₁е₁+…+a_dе_d +g₁g₁+…+g_mg_m = 0 Þ

a₁=…=a_d=g₁=…=g_m=0, так как {e₁ ,…,e_d,g₁ ,…,g_m} – базис подпространства L₂. Следовательно, векторы

{е₁,…,е_d, f₁,…, f_k, g₁,…, g_m } линейно независимы, и

dim(L₁ + L₂)= d + k + m = dimL₁ + dim L₂ - dim(L₁ 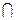L₂).

ÿ

Date: 2015-09-25; view: 319; Нарушение авторских прав