Доказательство. 1. Докажем существование разложения

1. Докажем существование разложения. Пусть

w(х)= 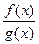, и g(x) = p₁(x) 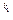… p_r(x) 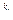- разложение на простые множители, p_i(x) ≠ p_j(x) при i ≠ j, и h(x) = p₂(x) 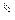… p_r(x) 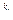. Тогда w(х)= 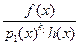. Вычтем из w(х) простейшую дробь 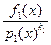с неопределенным пока числителем f₁(x):

w(х) - 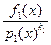= 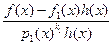. Покажем теперь, что можно подобрать f₁(x) так, чтобы числитель f(x) – f₁(x)h(x) делился на р₁(х). В самом деле, так как h(x) и p₁(x) – взаимно простые, то по утверждению 1 из 10.4 существуют многочлены u(x) и v(x) такие, что h(x)u(x) + p₁(x)v(x)= 1. После умножения этого равенства на f слева и справа получим f = fuh + p₁vf. В качестве f₁ можно было бы взять fu, но мы не знаем, будет ли ст.fи < ст.р₁. В случае, когда ст.fи ³ ст.р₁, разделим

fu на р₁ с остатком: fи = qр₁+ r₁, ст.r₁< ст.р₁. Тогда

f = fuh+ p₁vf = (qр₁+r₁)h + p₁vf = r₁h+ p₁(qh+ vf)= r₁h+ p₁ 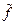, и можно взять f₁ = r₁. Теперь f(x) – f₁(x)h(x) делится на р₁(х), и ст.f₁<ст.р₁. Таким образом, w(х)= 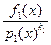+ 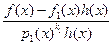= = 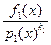+ 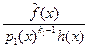. Далее такую же процедуру можно проделать с дробью 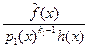или считать, что для неё утверждение выполнено по предположению индукции. Отсюда следует существование разложения рациональной функции на простейшие дроби.

2. Докажем единственность разложения. Пусть

w(х)= 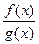= F(x)+ 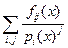= F(x)+ 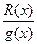Þ f = Fg + R, и ст.R < ст.g. Из однозначности деления с остатком получаем, что F и R определяются однозначно. Пусть теперь 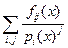= 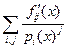- два разложения на простейшие дроби. Тогда 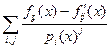= = 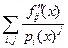0, где f¢¢_ij = f_ij - f¢_ij.

Если 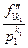, 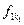¹ 0, - простейшая дробь в нашем разложении с наивысшей степенью многочлена р₁ в знаменателе, то общим знаменателем для суммы 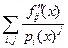будет 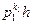, где h на р₁ не делится. Умножим равенство 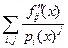= 0 на общий знаменатель. Получим: 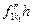+сумма всех остальных слагаемых, содержащих множитель р₁, = 0, то есть 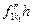+ р₁Н = 0. Но 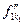и h не делятся на р₁. Мы получили противоречие. Отсюда следует единственность разложения на простейшие дроби.

ÿ

Лекция 24.

Date: 2015-09-25; view: 363; Нарушение авторских прав