Построение поля отношений

Пусть А – произвольное АКУ-кольцо без делителей нуля.

Рассмотрим множество М = {(a, b)| a, b Î A, b ¹ 0 }. Введем на М отношение p следующим образом: пусть по определению (a, b)p (с, d) Û (ad = bc).

Упражнение. Проверить, что p - отношение эквивалентности на М.

Пусть K= M ¤ p. Элементами множества K являются всевозможные классы cl_p(a, b), где (a, b) Î М. Будем обозначать cl_p(a, b) в виде . Очевидно, " и " с ¹ 0 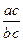= , так как (ac,bc)p(а,b) и bc ¹ 0.

I. Введем на множестве K операции сложения и умножения. Пусть по определению cl_p(a, b) + cl_p(с, d)= cl_p(ad+bc,bd), то есть + 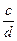= 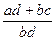, и cl_p(a, b)× cl_p(с, d)= cl_p(ac, bd), то есть × 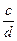= 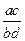. Очевидно, bd ¹ 0, то есть пары (ad+bc,bd), (ac, bd)Î М, и значит, классы cl_p(ad+bc,bd) и cl_p(ac, bd) определены.

Упражнение. Проверить корректность определения операций, то есть независимость определения от выбора представителей в классах. Иначе, если (a,b)p(a₁,b₁), (c,d)p(c₁,d₁), то необходимо проверить, что (ad+bc,bd)p (a₁d₁+b₁c₁,b₁d₁) и

(ac, bd)p (a₁c₁, b₁d₁).

II. Проверим, что на множестве K выполняются 9 свойств из определения поля.

2. Очевидно, " b ¹ 0 (0, b)p (0, 1), и 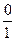= 0_K – нейтрал по сложению в K (проверить!).

3. Проверить, что – = .

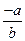6. Очевидно, " b¹ 0 (b, b)p(1, 1), то есть 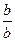= и = 1_K – нейтрал по умножению в K.

7. Очевидно, при а ¹ 0 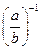= 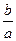, так как 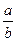× 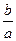= = 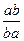1.

Упражнение. Проверить свойства 1, 4, 5, 8, 9 из определения поля.

Построенное нами поле K называется полем отношений

или полем частных для кольца А. Элементы поля K называются дробями.

Рассмотрим отображение j: А ® K такое, что "а Î A j(а)= 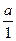. Очевидно, j(а₁)= j(а₂)Û 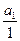= 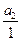Û (а₁,1)p(а₂,1)Û Û а₁= а₂, то есть j является инъекцией. Будем считать, что А инъективно вкладывается в K при помощи j, то есть будем отождествлять элементы вида 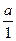в K с элементами а и считать, что A Í K. Тогда " 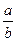Î K имеем 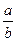= 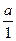× 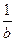= 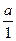× 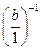= = а×b^-1 – привычное понимание дроби.

Date: 2015-09-25; view: 358; Нарушение авторских прав