Разложение многочлена на простые множители

в С [x] и в R [x].

1. Пусть f(x) Î C [x], ст. f(x)= п. Тогда по следствию к

основной теореме алгебры f(x) можно разложить в произведение п множителей 1-й степени, и значит, при п>1 f(x) – не простой многочлен. Следовательно, в С [x] простыми многочленами являются лишь многочлены 1-й степени, и наоборот, любой многочлен 1-й степени является простым.

2. Для f(x)= а_пх^п+ а_п-1х^п-1+…+ а₀ Î С [x] пусть по определению 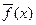= 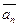х^п+ 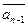х^п-1+…+ 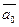, где все - комплексные числа, сопряженные к а_s. Очевидно, 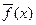= f(x) Û f(x)Î R [x],

и " z Î C = .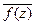

Пусть f(x)Î R [x]Ì С [x], ст. f(x)> 0, и f(z) = 0, z Î C. Тогда 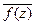= = f( 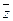)= = 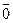0 Þ если z – корень многочлена f, то 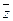- также корень f. Таким образом, множество комплексных недействительных корней многочлена разбивается на пары взаимно сопряженных. Если z = a + ib, 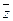=a - ib, то f(x)= (х – z)(x – 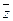)g(x), и (х – z)(x – 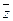)= х² – 2aх + (a² +b²) – простой многочлен в R [x], дискриминант которого (– 4b²)< 0. Следовательно, если ст. f(x)> 2, то f(x) – не простой многочлен, так как либо он имеет действительный корень и, соответственно, множитель 1-й степени, либо пару комплексно сопряженных недействительных корней и, соответственно, множитель 2-й степени. Значит, простые многочлены в R [x] – это либо многочлены 1-й степени, либо 2-й степени с отрицательным дискриминантом.

Замечание. Если f(x)Î R [x], ст.f(x)= п, и с₁,c_2,…,c_k – все действительные корни, z₁, 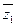,…,z_m, - все комплексные корни многочлена f(x), то k+2m = n, и значит, 1) если п – нечетное число, то k > 0, и действительные корни у f(x) существуют; 2) k º n (mod2), то есть числа k и n имеют одинаковую четность.

Лекция 23.

Date: 2015-09-25; view: 356; Нарушение авторских прав