Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Построение алгебры многочленов
|
|
Пусть Р – произвольное поле.
Определение. Многочленом с коэффициентами в поле Р
будем называть бесконечную строчку (a0,a1,a2,a3,…), где все компоненты a0,a1,a2,a3,…Î P и почти все a i (то есть все, за исключением конечного числа) равны 0. Множество многочленов будем обозначать P [x].
I. Определим на множестве P [x] операции:
пусть для f = (a0,a1,a2,…), g = (b0, b1, b2,…)Î P [x], lÎ P по определению l×f = (la0, la1, la2,…),
f + g = (a0 +b0, a1 +b1, a2 +b2,…), f×g =(g0, g1, g2,…), где
g0 =a0b0 , g1 = a0b1+a1b0, g2 =a0b2+a1b1 +a2b0, и " k ³ 0 gk =a0bk+a1bk-1+a2bk-2 + …+akb0 =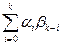 
= 
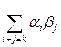. Очевидно, у строчек l×f, f + g, f×g также почти все компоненты равны нулю, то есть l×f, f + g, f×g содержатся в P [x].
II. Легко проверить, что для определенных нами операций выполнены свойства АКУ-кольца (см. Лекцию 11):
1. (f + g) + h = f + (g + h) " f, g, h Î P [x],
2. $ элемент 0 Р[x] Î P [x], 0 Р[x] = (0,0,0,…) такой, что 0 Р[ x] + f = f + 0 Р[ x] = f " fÎ P [x],
3. " fÎ P [x] $ элемент - fÎ P [x] такой, что (- f)+f = 0 Р[x],
4. f + g = g + f " f, g Î P [x],
5. (fg)h = f(gh) " f, g, h Î P [x],
6. $ элемент 1 Р[x] Î P [x], 1 Р[x] = (1,0,0,…) такой, что
1 Р[x] ×f = f×1 Р[x] = f " fÎ P [x],
8. fg = g f " f, g Î P [x],
9. (f + g)h = fh +gh " f, g, h Î P [x],
а также выполнены свойства линейного пространства:
v. l(f+g) = lf+lg " f, gÎ P [x], "lÎ P,
vi. (l+m)f = l f+m f " fÎ P [x], "l, mÎ P,
vii. (lm)f = l(m f) " fÎ P [x], "l, mÎ P,
viii. 1×f = f " fÎ P [x],
и свойство l(fg) = (lf)g = f(lg) " f, gÎ P [x], "lÎ P.
Проверим, например, свойство 5. Пусть f = (a0,a1,a2,…), g = (b0, b1, b2,…), h = (g0, g 1, g2,…), fg =(d0, d1, d 2,…). Тогда dк = 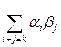, и s-я компонента строчки (fg)h равна
= 
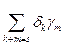, то есть совпадает с s-й компонентой строчки f(gh) " s. Отсюда (fg)h = f(gh).
Упражнение. Доказать остальные свойства.
Таким образом, мы получаем, что P [x] является АКУ-кольцом, линейным пространством и алгеброй над полем Р
(см. Лекцию 18, п.9.1).
Определение. Пусть f = (a0,a1,a2,…), и ak ¹ 0, а при m > k все am = 0. Тогда мы будем говорить, что степень многочлена f равна k и писать ст.f = k или deg.f = k. Будем считать по определению, что ст.0 Р[ x] = - ¥.
Обозначим многочлен (0,1,0,0,0,…) через х. Тогда легко проверить, что х2=(0,0,1,0,0,…), х3= (0,0,0,1,0,…),…, и значит, f = (a0,a1,a2,…)= (a0,0,0,0,…)+(0,a1,0,0,…)+(0,0,a2,0,…)+…=
= a0(1,0,0,0,…) + a1(0,1,0,0,…) + a2(0,0,1,0,…) + …= a01 Р[x] + +a1х +a2х2+… Если в этом выражении не писать нулевые слагаемые и множитель 1 Р[x], то f = a0 + a1х + a2х2+ …+akхk, где k = ст.f.
Теорема. ст.(fg) = ст.f + ст.g.
Доказательство. Если f = 0 Р[x] или g = 0 Р[x], то левая и правая части равенства равны -¥, и утверждение теоремы верно. Если же ст.f ³ 0, f=akхk + ak-1хk-1+…+ a1х + a0, ak¹ 0, ст.g ³ 0, g= bmхm + bm-1хm-1+…+ b1х + b0, bm¹ 0, то
fg = akbmхk+m+…, и akbm ¹ 0 Þ ст.(fg) = k + m = ст.f + ст.g.
ÿ
Следствие. В кольце Р [x] нет делителей нуля.
При построении кольца многочленов вместо поля Р можно аналогичным образом использовать произвольное АКУ-кольцо А. В этом случае мы получим АКУ-кольцо многочленов А [x] с коэффициентами в кольце А. Так, например, если А = Z, то мы получим кольцо многочленов Z [x] с целыми коэффициентами. Если А = Р [x1], то кольцо А [x2] = Р [x1][x2] = = Р [x1,x2] – это кольцо многочленов от двух переменных с коэффициентами в поле Р.
Date: 2015-09-25; view: 380; Нарушение авторских прав