Следствия. 1. Множество делителей для f и g совпадает с множеством делителей для r1 и r2 , с множеством делителей для r2 и r3

Определение. Элемент р кольца K называется простым, если из разложения р = rs, r, s Î K, следует, что или r |1 или s |1. В кольце P [x] простые многочлены называют ещё неприводимыми многочленами.

Определение. Говорят, что в кольце К разложение на простые множители квазиоднозначно, если " а Î K, а ¹ 0, из существования разложений на простые множители

а = р₁р₂…р_k = q₁q₂…q_s (где все р_i, q_j – простые элементы кольца K) следует, что k = s, и, может быть, после перенумерации мы можем получить р _i = q _ic _i "i, где c _i | 1.

Теорема. В кольце P [x] разложение на простые многочлены существует.

Доказательство от противного. Пусть в P [x] разложение

на простые многочлены не существует. Значит, $ fÎ P [x], для которого не существует разложение на простые многочлены. Следовательно, f – не простой (иначе разложение на простые многочлены для f существует и состоит из одного множителя). Если f – не простой, то f = а₁а₂, где а₁, а₂Î P [x], ст.а₁> 0, ст.а₂ > 0, и либо для а₁, либо для а₂ разложение на простые множители не существует. Пусть не существует разложение на простые многочлены для а₁. Очевидно,

ст.f > ст.а₁, и а₁ - не простой Þ а₁ = b₁b₂, где b₁, b₂Î P [x], ст.b₁> 0, ст.b₂ > 0, и либо для b₁, либо для b₂ разложение на простые множители не существует. Пусть не существует для b₁ Þ ст.a₁ > ст.b₁, и b₁ - не простой Þ b₁ = c₁c₂ и т.д. С одной стороны процесс никогда не закончится, а с другой стороны ст.f > ст.а₁> ст.b₁>…, и процесс до бесконечности продолжаться не может. Получили противоречие.

ÿ

Лемма. Пусть h и f - взаимно простые, и h | (fg). Тогда h | g.

Доказательство. Так как h и f - взаимно простые, то hf является их наименьшим общим кратным, а fg - их общее кратное по условию леммы. По теореме из 10.3 (hf) |(fg), то есть h | g.

ÿ

Теорема. В кольце P [x] разложение на простые многочлены квазиоднозначно.

Доказательство. Пусть для некоторого f Î P [x] имеем

разложения f = р₁р₂…р_k = q₁q₂…q_s (где все р_i, q_j – простые многочлены кольца P [x]). Очевидно, р₁| q₁(q₂…q_s), и если р₁ и q₁ – взаимно простые многочлены, то по лемме р₁| (q₂…q_s). Аналогично, если р₁ и q₂ – взаимно простые, то р₁| (q₃…q_s), и т.д. В конце концов мы получим, что существует i такое, что р₁ и q_i – не взаимно простые, то есть q_i = с₁р₁, с₁Î P. Сократив равенство р₁р₂…р_k = q₁q₂…q_s на р₁, получим

р₂…р_k = с₁q₁q₂… 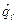…q_s (крышка над q_i означает, что множи-

тель q_i отсутствует). Далее переходим к р₂. Как и ранее, получим, что для р₂ существует q_j такой, что q_j = с₂р₂, с₂Î P. Опять сокращаем равенство на р₂ и переходим к р₃, и т.д. После сокращения на все левые множители р₁, р₂,…, р_k, получим, что k = s и 1 = с₁с₂…с_k.

ÿ

Упражнение. Сформулировать и доказать существование и однозначность разложения на простые множители в N.