Кратные корни многочлена

Далее в 10.7 будем считать, что char P = 0.

Определение. Пусть f(x)= p(x)^kg(x), где p(x) - простой многочлен в P [x], и p(x) не делит g(x). Тогда k – называется кратностью множителя p(x) в разложении f(x). Если k ³ 2, то множитель p(x) называется кратным. Если р(х) = х – а, то есть f(x)= (x – а)^kg(x), и (х – а) не делит g(x), то k – называется кратностью корня а многочлена f(x). Если k ³ 2, то корень а называется кратным, а если k = 1, то корень а называется простым.

Теорема. Если кратность простого множителя p(x) в раз-

ложении f(x) равна k, то кратность p(x) в разложении f¢(x) равна k – 1.

Доказательство. Так как f¢(x)=kp(x)^k-1p(x)¢g(x)+p(x)^kg(x)¢= = p(x)^k-1(kp(x)¢g(x)+p(x)g(x)¢), то p(x)^k-1 | f¢(x). Покажем, что p(x) не делит (kp(x)¢g(x)+p(x)g(x)¢). В самом деле, если мы предположим, что p(x)| (kp(x)¢g(x)+p(x)g(x)¢), то получим, что p(x)| (kp(x)¢g(x)). Но p(x) и g(x) – взаимно простые Þ p(x)| p(x)¢ - противоречие, так как ст.p(x)¢ = ст.p(x) – 1.

ÿ

Теорема. У f(x) существуют кратные простые множители тогда и только тогда, когда f и f¢ не взаимно простые.

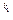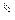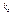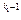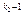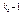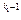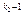Доказательство. Пусть f(x)= р₁ р₂ …р_s - разложение f на простые множители. Тогда f¢(x)= р₁ р₂ … р_s h(x), и h(x) не делится на р_i "i. Следовательно, D= р₁ р₂ …р_s 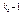является наибольшим общим делителем для f и f¢. Таким образом, f и f¢ не взаимно простые, то есть D ¹ 1 Û $ k_i> 1.

ÿ

Если необходимо решить уравнение f(x)= 0, и многочлен f(x) содержит кратные множители, то мы можем перейти к эквивалентному уравнению меньшей степени следующим образом. С помощью алгоритма Евклида найдем D – наибольший общий делитель для f и f¢. Затем разделим f на D:

f ¤ D = р₁р₂…р_s. Очевидно, уравнение f ¤ D = 0 эквивалентно первоначальному уравнению, то есть имеет те же корни. Операция перехода к уравнению f ¤ D = 0 называется освобождением от кратных множителей или освобождением от кратных корней.

Date: 2015-09-25; view: 709; Нарушение авторских прав