Решение и исследование систем линейных уравнений по Гауссу

Рассмотрим СЛУ вида (4.1). Расширенную матрицу системы приведем с помощью ЭП к ступенчатому виду

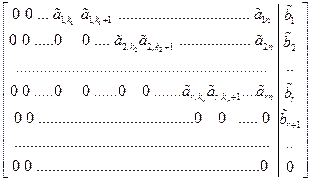. (4.2)

Здесь ранг основной матрицы системы равен rgA = r.

1. Если ¹ 0, то ранг расширенной матрицы rg 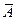= r+1, и (r+1) -е уравнение системы ступенчатого вида имеет вид

0 х₁ + … + 0 х_n = b_r+1, то есть несовместно. Значит, и вся СЛУ несовместна.

2. Если = 0, то ранг расширенной матрицы rg 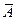= rgA = r. Покажем, что в этом случае СЛУ совместна. Назовем все неизвестные , i = 1,…,r, с которых начинаются ступеньки, главными, а все остальные (n – r) неизвестных – свободными. В системе ступенчатого вида, поднимаясь снизу вверх с r -го уравнения и до первого, выразим главные неизвестные через свободные: ,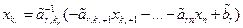

. Затем в правую

часть этой формулы подставим выражение для главного

неизвестного 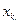из предыдущей формулы – получим выражение главного неизвестного 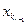только через свободные неизвестные. После этого из (r-2)- й строки системы (4.2) выразим и в правую часть формулы подставим выражения для главных неизвестных 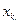, 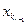из предыдущих формул – получим выражение главного неизвестного только через свободные неизвестные. Затем переходим к (r-3)- й строке системы (4.2) и так далее до 1-й строки.

На полученные r формул можно смотреть двояко. Во-первых, можно считать, что это СЛУ, равносильная первоначальной СЛУ (4.1) и записанная специфическим удобным способом, при котором некоторые неизвестные (главные) выражены через другие (свободные). Во-вторых, эти формулы можно считать общим решением системы (4.1), в котором свободные неизвестные являются параметрами и принимают произвольные значения из поля Р, а главные неизвестные однозначно находятся по нашим формулам. Для эстетов, которым не нравится второй взгляд, можно уточнить этот второй взгляд введением других букв. Присвоим свободным (n – r) неизвестным произвольные значения t₁, t₂,…,t_n-r из поля P, a значения главных неизвестных найдем по нашим формулам. Полученный набор значений неизвестных и будет решением системы (4.1).

Таким образом, нами доказана

Теорема Кронекера-Капелли. С истема (4.1) совместна тогда и только тогда, когда rg A = rg .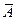

Если r = n, то есть свободных неизвестных нет, и все неизвестные – главные, а матрица ступенчатого вида в (4.2) – треугольная, то система (4.1) имеет единственное решение, то есть является определенной. Если r < n, то свободные неизвестные существуют, и система имеет более одного решения, то есть является неопределенной. Если поле Р – бесконечное, то при r < n совместная СЛУ имеет бесконечно много решений.

Date: 2015-09-25; view: 373; Нарушение авторских прав