Упражнения

1. Доказать, что отношение R на множестве Х рефлексивно

Û R Ê D_X.

2. Доказать, что отношение R – симметрично Û R^-1 – симметрично Û R = R^-1.

3. Доказать, что отношение R – транзитивно Û R²Í R (здесь R²= R*R).

4. Доказать, что пустое отношение Æ – симметрично и транзитивно.

5. Найти множества, для которых пустое отношение Æ – рефлексивно.

6. Доказать, что на множестве Х наибольшее отношение

R= X´X рефлексивно, симметрично и транзитивно, и, следовательно, является отношением эквивалентности.

7. Доказать, что пересечение рефлексивных отношений – рефлексивно, пересечение симметричных отношений – симметрично, пересечение транзитивных отношений – транзитивно, пересечение отношений эквивалентности - отношение эквивалентности.

8. Доказать, что объединение рефлексивных отношений – рефлексивно, объединение симметричных отношений – симметрично. Привести пример транзитивных отношений, объединение которых не транзитивно.

9. Привести пример симметричных отношений, компози-

ция которых не симметрична. Привести пример транзитивных отношений, композиция которых не транзитивна.

Определение. Для отношения эквивалентности p на мно­же­стве Х определим класс элемента хÎ Х как

cl_p x = { yÎ Х| yp x }. Когда ясно, какое отношение эквивалентности имеется ввиду, будем обозначать класс элемента х также cl x или .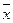

Утверждения. Пусть p - отношение эквивалентности. Тогда

1) " хÎ Х хÎ cl_p x.

2) Если хÎ cl_p y, то yÎ cl_p x.

3) Если yÎ cl_p x, то cl_p y Í cl_p x.

4) Если yp x, то cl_p y = cl_p x.

Доказательство 1) следует из определения рефлексивности, 2) – из определения симметричности, 3) – из определения транзитивности, 4) – из утверждений 2), 3).

Теорема. Если на множестве Х задано отношение эквивалентности p, то множество Х разбивается в объединение непересекающихся классов эквивалентных элементов, то есть X = 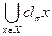, где " x, yÎ X либо cl_p х ∩ cl_p y = Æ, либо cl_p х = cl_p y. Наоборот, любое разбиение множества Х в объединение непересекающихся подмножеств получается из некоторого отношения эквивалентности, которое определено однозначно, то есть если Х = U Х_i, где Х_i ∩ Х_j = Æ при i ¹ j, то $! отношение эквивалентности p такое, что "i Х_i = cl_p х_i, где х_iÎ Х_i.

Date: 2015-09-25; view: 413; Нарушение авторских прав