
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Упражнения. 1. Проверить, что, s s+1x =s x, s s+2x =s 2x, s -1x = s s-1x, , s(О(x))=О(х), s k(О(х)) = О(x), О(sx) =О(х)
|
|
1. Проверить, что, s s+1x =s x, s s+2x =s 2x, s -1x = s s-1x, …, s(О(x))=О(х), s k(О(х)) = О(x), О(sx) =О(х), О(s kх) = О(x), О(х) = {s kx| k =0,1, 2,…, s-1 } = {s kx| k Î Z }.
2. Проверить, что циклы разных элементов либо не пересекаются, либо совпадают.
Таким образом, множество Х разбивается в объединение непересекающихся циклов.
Пусть х = a1, s x = a2 , s 2x = a3 , s 3x = a4 ,…, s s-1x = as, и соответственно цикл О(х) ={a1, a2 ,.., as}. Тогда s(О(x))= О(х), и s на О(x) является биекцией, которую можно записать в виде таблицы 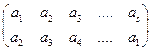 или в виде таблицы с одной строкой: (a1, a2, a3,…, as). Запись s в виде такой строки означает, что s a1= a2, s a2= a3 ,…,s as-1= as, s as= a1 . Записывая подстановку на каждом цикле в виде одной строки, получим циклическую запись подстановки. Так, например, подстановка
или в виде таблицы с одной строкой: (a1, a2, a3,…, as). Запись s в виде такой строки означает, что s a1= a2, s a2= a3 ,…,s as-1= as, s as= a1 . Записывая подстановку на каждом цикле в виде одной строки, получим циклическую запись подстановки. Так, например, подстановка
s = 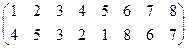 в циклической записи имеет вид s =(1, 4, 2, 5)(3)(6, 8, 7).
в циклической записи имеет вид s =(1, 4, 2, 5)(3)(6, 8, 7).
Определение. Транспозицией будем называть подстановку tij такую, что tij (i)= j, tij (j) = i, tij (k) = k при k ¹ i, k¹j.
Очевидно, tij-1 = tij, tij2 = tij.
Утверждение. Любую подстановку s Î Sn, п ³ 2, можно разложить в композицию транспозиций.
Доказательство по индукции.
1. При п =2 утверждение очевидно, так как S2 состоит из двух элементов: id и tij.
2. Пусть для п – 1 утверждение верно. Рассмотрим s Î Sn. Пусть s(п) = q, и s1 = tqn  s. Тогда s1 (n) = n, и s1 – биекция множества {1, 2, 3, …, n -1 } из (п-1)- го элемента. По предположению индукции можно считать, что для s1 утверждение верно, то есть s1=t1
s. Тогда s1 (n) = n, и s1 – биекция множества {1, 2, 3, …, n -1 } из (п-1)- го элемента. По предположению индукции можно считать, что для s1 утверждение верно, то есть s1=t1  t2
t2 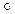 …
… 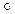 tr - композиция транспозиций. Но s = tqn-1
tr - композиция транспозиций. Но s = tqn-1 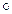 s1 = tqn
s1 = tqn 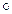 s1 = tqn
s1 = tqn 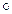 t1
t1 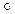 t2
t2 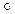 …
… 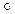 tr - композиция транспозиций.
tr - композиция транспозиций.
Очевидно, разложение подстановки в композицию транспозиций неоднозначно.
На практике очень легко раскладывать подстановку в произведение транспозиций, если она задана в циклической записи. Так, например, легко проверить, что
(1, 3, 7, 2, 4)(5, 6)(8) = t13 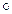 t37
t37 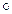 t72
t72 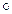 t24
t24 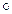 t56.
t56.
Будем говорить, что в последовательности чисел i1, i2 ,..,in два числа ik и il образуют инверсию, если ik > il, но ik расположено левее il. Подстановка s = 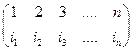 называется четной, если количество инверсий в её нижней строке
называется четной, если количество инверсий в её нижней строке
четно, и s называется нечетной, если количество инверсий в
её нижней строке нечетно.
Утверждение. Если количество инверсий в нижней строке подстановки s равно m, то s можно разложить в произведение m транспозиций.
Доказательство. Пусть два соседних элемента ik и ik+1 в нижней строке подстановки s образуют инверсию. Тогда
s1= 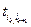
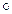 s =
s = 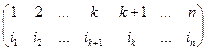 , и число инверсий в нижней строке у s1 равно m – 1. Продолжая эту процедуру далее, получим, что существуют транспозиции t1 ,t2 , …,tm такие, что подстановка tm
, и число инверсий в нижней строке у s1 равно m – 1. Продолжая эту процедуру далее, получим, что существуют транспозиции t1 ,t2 , …,tm такие, что подстановка tm 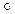 tm-1
tm-1 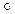 …
… 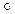 t1
t1 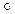 s не имеет инверсий в нижней строке, то есть tm
s не имеет инверсий в нижней строке, то есть tm 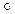 tm-1
tm-1 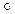 …
… 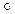 t1
t1 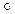 s = id. Умножая последнее равенство слева на tm, затем на tm-1 и так далее до t1, и учитывая, что все ti2= id, получим, что s = t1
s = id. Умножая последнее равенство слева на tm, затем на tm-1 и так далее до t1, и учитывая, что все ti2= id, получим, что s = t1  t2
t2  …
…  tm.
tm.
Лекция 4.
Date: 2015-09-25; view: 453; Нарушение авторских прав