Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Подстановки
|
|
Пусть Х – конечное множество, Х = {х1, х2,…, хn }. Группу подстановок S(X) в этом случае мы будем обозначать Sn. Подстановку s множества Х можно записывать в виде таблицы s =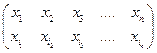 
, где в нижней строке стоят каким-то образом переставленные элементы множества Х. Такая таблица означает, что s(х1)= 
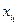, s(х2)= 
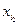, s(х3)= 
…
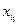Так как s - инъекция, то все элементы нижней строки различные. Так как s - сюръекция, то в нижней строке присутствуют все элементы множества Х. То есть, нижняя строка – это перестановка множества Х. Таким образом, различных подстановок существует ровно столько, сколько имеется различных перестановок множества Х, то есть n!, и, значит, группа Sn подстановок множества из п элементов состоит из n! элементов.
Упражнение. Доказать, что для конечного множества Х
из инъективности s следует её сюръективность, а из сюръективности - инъективность.
Чаще всего мы будем считать, что Х = {1, 2, 3, …, n }. В этом случае подстановки мы будем записывать в виде
s =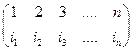 
, где i1, i2,…, in - перестановка чисел 1, 2, 3, …, п.
Для композиции подстановок s1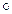 
s2 вначале выполняется подстановка s2, а затем s1, а для композиции s1*s2 - вначале s1, а затем s2.
Пусть s k =s 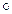s … s 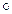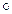- произведение k множителей. Так как Х - конечное множество, то " xÎ Х "s Î Sn {s kx | kÎ N } – конечное подмножество в Х, то есть $ k¹ m такие, что s k x = s m x. Тогда, если k> m, то, очевидно,
s k-m x = x. Пусть s – наименьшее натуральное число такое, что s sx = x. Тогда подмножество {x, s x, s 2x, s 3x,…,s s-1x} будем называть циклом, порожденным элементом х, и обозначать O(х). Очевидно, все элементы в O(х) – различны, то есть O(х) состоит из s элементов. Будем считать, что по определению s 0 = id, s0x= х.
Date: 2015-09-25; view: 388; Нарушение авторских прав