
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Упражнения. 1. Проверить, что DA*S = S, S*DB =S S Í A´B
|
|
1. Проверить, что DA*S = S, S*DB =S "S Í A´B.
2. Проверить, что
(S1*S2)*S3 = S1*(S2*S3) " S1 Í A´B, S2 Í B´C, S3 Í C´D.
3. Проверить, что (S -1) -1 = S " S Í A´B.
4. Проверить, что (S1*S2) -1 = S2-1 * S1-1 " S1 Í A´B, S2 Í B´C.
5. Доказать, что если отображения F1 из A в B и F2 из B в C являются инъекциями, то F2 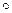 F1 – инъекция.
F1 – инъекция.
6. Доказать, что если отображения F1 из A в B и F2 из B в C являются сюръекциями, то F2 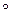 F1 – сюръекция.
F1 – сюръекция.
7. Доказать, что если отображения F1 из A в B и F2 из B в C являются биекциями, то F2 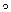 F1 – биекция.
F1 – биекция.
8. Доказать, что для отображения F из A в B соответствие F -1 будет отображением из B в A Û F – биекция. В этом случае F -1 - также биекция, и F* F -1 =DA, F -1* F =DB.
9. Доказать, что для отображения F из A в B
уравнение Fx= b имеет £ 1 решения "b Û F – инъекция,
уравнение Fx= b имеет ³1 решения "b Û F – сюръекция,
уравнение Fx=b имеет ровно одно решение "b Û F – биекция.
10. Доказать, что отображение F из A в B является инъекцией Û F* F -1 =DA.
11. Доказать, что отображение F из A в B является сюръекцией Û F -1* F =DB.
Пусть S(X) – множество биекций множества Х. Тогда
I. " f, gÎ S(X) f 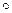 g Î S(X) (из упр. 5),
g Î S(X) (из упр. 5),
II. 1. " f, g, hÎ S(X) (f 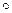 g)
g) 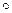 h = f
h = f 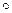 (g
(g 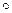 h) (из упр. 2),
h) (из упр. 2),
2. $ DXÎ S(X) (очевидно, DX – биекция из Х в Х и DX(х)=х " хÎ X) и " fÎ S(X) f 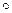 DX = DX
DX = DX 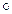 f = f (из упр.1). Биекция DX обозначается ещё idX или id.
f = f (из упр.1). Биекция DX обозначается ещё idX или id.
3. " fÎ S(X) $ f -1Î S(X) и f -1 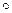 f = f
f = f 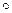 f -1= DX (из упр.6).
f -1= DX (из упр.6).
Далее множества с такими свойствами мы будем называть группами. Таким образом, S(X) - группа.
Date: 2015-09-25; view: 361; Нарушение авторских прав