Комплексные числа

Будем считать известными множества натуральных чисел N, целых чисел Z, рациональных чисел Q, действительных чисел R.

Определение. Комплексным числом будем называть упорядоченную пару действительных чисел (a,b), a,b Î R.

Множество комплексных чисел будем обозначать буквой С.

С = {(a,b), a,b Î R }.

I. Определим на множестве С операции:

1. по определению (a,b)+ (с,d) = (a+с, b+d) – операция сложения,

2. по определению (a,b)× (с,d) = (aс - bd, ad+bc) – операция умножения,

3. для с Î R по определению с× (a,b)= (ca, cb) – операция умножения комплексных чисел на действительные.

II. Утверждение. Для определенных на С операций выполняются свойства:

1. (z₁ + z₂) + z₃ = z₁ +(z₂ + z₃) " z₁, z₂, z₃ Î C, z₁ =(a₁,b₁),

z₂ = (a₂,b₂), z₃ = (a₃,b₃),

2. $ элемент 0 _С = (0,0)Î C такой, что 0 _С +z = z + 0 _С = z " zÎ C. 0 _С называется нейтральным элементом в C по сложению.

3. " z Î C, z =(a,b), $ z¢ Î C такой, что z+ z¢ = 0 _С. В самом деле, z¢ = (- a, - b). z¢ обозначается как - z и называется элементом, противоположным к z.

4. z₁ + z₂ = z₂ + z₁ " z₁, z₂ Î C,

5. (z₁ z₂) z₃ = z₁ (z₂ z₃) " z₁, z₂, z₃ Î C,

6. $ элемент 1 _С = (1,0)Î C такой, что 1 _С × z = z × 1 _С = z " zÎ C. 1 _С называется нейтральным элементом в С по умножению или единицей.

7. " z Î C, z ¹ 0 _С, z =(a,b), $ z₁ Î C такой, что z z₁ = 1 _С. В самом деле, z₁ = (a/(a² + b²), - b/(a² + b²)). z₁ обозначается как z^-1 и называется элементом, обратным к z.

8. z₁ z₂ = z₂ z₁ " z₁, z₂ Î C,

9. (z₁ +z₂)z₃ = z₁ z₃ + z₂ z₃, z₁(z₂ + z₃)= z₁ z₂+ z₁z₃ " z₁, z₂, z₃Î C.

i. c(z₁ + z₂) = cz₁ + cz₂ " z₁, z₂ Î C, " c Î R,

ii. (c + d)z = cz + dz " c, d Î R, " zÎ C,

iii. (c d)z = c(dz) " c, d Î R, " zÎ C,

iv. 1 _С z = z " zÎ C.

Очевидно, все эти свойства следуют из определений операций и свойств действительных чисел, которые мы считаем известными.

Упражнение. Доказать свойства 1 ¸ 9 и i ¸ iv.

Множество (не обязательно числовое), на котором

I. определены операции, обозначаемые знаками + и ×,

II. и для которых выполнены свойства 1 ¸ 9, называется полем.

Очевидно, полями являются множества Q и R. Теперь мы видим, что множество С также является полем.

Обозначим число (0, 1)Î C буквой i. Число i называется мнимой единицей. Очевидно, " zÎ C, z = (a,b) = a (1, 0) + + b (0, 1)= a× 1 _С + b i. Обычно единицу в качестве множителя не пишут. Поэтому и мы будем записывать число z в виде

z = a + b i, а единицу 1 _С, когда это не вызовет недоразумений, мы будем записывать в виде 1.

Легко видеть, что i² = - 1. Для комплексного числа

z = a + b i будем называть комплексное число a - b i комплексно сопряженным к z и обозначать 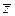. Очевидно,

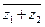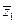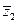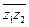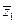
а) = + , б) = 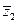, в) z 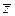= a² + b².

Определение. Модулем комплексного числа z = a + b i называется число | z | = .

Так как z 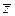= | z | ², то | z₁ z₂ | ² = z₁z₂ 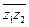= z₁z₂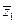 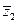= | z₁ | ² | z₂ | ²,

и | z₁ z₂ | = | z₁ | ×| z₂ |.

Комплексное число a + b i можно изображать точкой на плоскости с координатами (a, b) или вектором на плоскости с координатами (a, b). Легко видеть, что комплексные числа складываются как векторы по правилу параллелограмма (или по правилу треугольника). Очевидно (см. рис.),

a + b i = r cosj +r sinj ×i = r(cosj +i sinj).

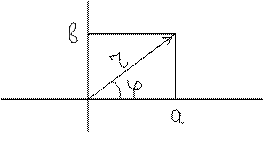
Запись комплексного числа в виде r(cosj +i sinj) называется тригонометрической формой записи. Угол j называется аргументом комплексного числа (определен неоднозначно). Очевидно, r = | z |.

Легко проверить, что r₁(cosj₁+i sinj₁)× r₂(cosj₂+i sinj₂)=

= r₁r₂(cos(j₁+j₂)+i sin(j₁+j₂)). Отсюда следует

формула Муавра: (cosj +i sinj)ⁿ = cos nj + i sin nj,

а также ещё раз мы получаем, что | z₁ z₂ | = r₁r₂ = | z₁ | ×| z₂ |.

Date: 2015-09-25; view: 324; Нарушение авторских прав