Комбинаторика

А.М. Попов

ЛЕКЦИИ ПО ЛИНЕЙНОЙ АЛГЕБРЕ

Для студентов I курса бакалавриата, обучающихся по направлениям «Прикладная математика. Информатика», «Математика. Компьютерные науки», «Математика. Прикладная математика»

Москва

Издательство Российского университета дружбы народов

У т в е р ж д е н о

РИС Ученого совета

Российского университета

дружбы народов

Попов А.М.

Лекции по линейной алгебре. - М.: Изд-во РУДН, 2007. – 183 с.

Вошедшие в Лекции разделы изучаются в курсе алгебры на математических специальностях бакалавриата.

Для студентов I курса бакалавриата по направлениям «Прикладная мате­матика. Информатика», «Математика. Компьютерные науки», «Математика. Прикладная математика».

Подготовлено на кафедре дифференциальных уравнений и математической физики.

© А.М. Попов, 2007

© Издательство Российского университета дружбы народов, 2007

Лекция 1.

КОМБИНАТОРИКА. БИНОМ НЬЮТОНА

Комбинаторика.

Пусть Х = {х₁, х₂, …, х_n } – множество из n элементов.

Определение. Размещением из n элементов по k называется упорядоченное подмножество, состоящее из k элементов, выбранных из множества Х. Подмножества, отличающиеся порядком, считаются различными.

Количество таких размещений обозначается 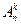и называется коротко количеством размещений из п по k.

Пример. {х₃, х₂, х₅ }, {х₃, х₂, х₄ }, {х₂, х₃, х₄ } – различные размещения из п по 3.

Мы будем записывать также размещения в виде х₃ х₂ х₅ ;

х₃ х₂ х₄; х₂ х₃ х₄ .

Определение. Сочетанием из n элементов по k называется (неупорядоченное) подмножество, состоящее из k элементов, выбранных из множества Х. Подмножества, отличающиеся порядком, считаются одинаковыми.

Количество таких сочетаний обозначается 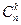и называется коротко количеством сочетаний из п по k.

Пример. {х₁, х₂}, {х₁, х₃}, {х₁, х₄}, {х₂, х₃}, {х₂, х₄},

{х₃, х₄} – все сочетания из 4 по 2.

Мы будем записывать также сочетания в виде х₁ х₂ , х₁ х₃, х₁ х₄ и т.д.

Определение. Перестановкой из n элементов называется размещение из п элементов по п.

Количество таких перестановок обозначается P_n.

Пример. {х₁, х₂, х₃}, {х₂, х₃, х₁}, {х₃, х₁, х₂},{х₂, х₁, х₃},

{х₃, х₂, х₁}, {х₁, х₃, х₂} – все перестановки из трёх элементов.

Утверждение 1.1. 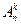= п(п -1)(п – 2)…(п – k + 1).

Доказательство индукцией по k (для произвольного п,

k£ п).

k = 1. Очевидно, 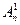= п, так как размещениями из п по 1 являются подмножества в Х, состоящие из одного элемента, а количество таких подмножеств равно количеству элементов в Х, то есть п.

Пусть утверждение верно для k - 1. То есть " m £ k-1

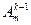= m(m -1)(m – 2)…(m – k + 2).

Докажем его для k. Рассмотрим k мест:

. Произвольное размещение из п по

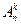k получается размещением на 1-е место любого из п элементов множества Х (таких возможностей имеется п), а на оставшиеся k - 1 мест - произвольного размещения из оставшихся m = n – 1 элементов множества Х (таких размещений имеется ). Отсюда = п × и по предположению индукции 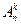= п × = n×(n -1)(n –2)…(n – k + 1)= n! /(n – k)!.



Следствие. P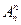_n = = n!

Утверждение 1.2. 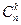= n(n -1)(n – 2)…(n – k + 1) / k!.

Доказательство. Так как все размещения из п по k получаются выборками из множества Х различных сочетаний из k элементов, а затем их всевозможными перестановками, то

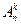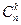= × P_k Þ 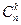= 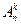/ P_k = n(n -1)(n – 2)…(n – k + 1) / k! =

= n! /((n – k)!× k!).

Утверждение 1.3. а) 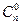= = 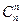1, б) = ,

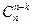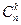в) = + .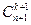

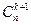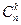Упражнение. Доказать утверждение с помощью формул.

Доказательство утверждения 1.3 без формул (для умных, но ленивых).

а) Очевидно, из п элементов ничего не выбирать или выбрать все элементы можно только одним способом.

б) Очевидно, каждому выбранному сочетанию из п по k соответствует сочетание оставшихся в Х п – k элементов, и количество сочетаний выбранных элементов равно количеству сочетаний оставшихся элементов.

в) сочетания из п + 1 элементов по k + 1 можно выбирать двумя способами: или выбрать все k + 1 элементов из первых п элементов – это можно сделать 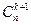способами, или обязательно включить в сочетание (п + 1)- й элемент, а остальные k элементов выбирать из первых п элементов – это можно сделать 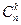способами.



Date: 2015-09-25; view: 354; Нарушение авторских прав