
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема о движении центра масс
|
|
Центром масс или центром инерции системы является геометрическая точка, положение которой определяется в каждый момент времени:
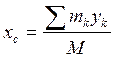 ,
, 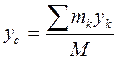 ,
,  , (8.1) где М – масса системы, равная сумме масс всех точек системы;
, (8.1) где М – масса системы, равная сумме масс всех точек системы;
mk-- масса произвольной точки Mk;
xk, yk, zk – координаты произвольной точки Mk системы.
В однородном поле земного тяготения центр масс совпадает с центром тяжести.
Центр масс существует для любой механической системы независимо от действующих сил.
Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложен все внешние силы, действующие на систему (теорема о движении центра масс).
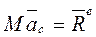 , (8.2) где М—масса системы;
, (8.2) где М—масса системы;
ac—ускорение центра масс;
 -- главный вектор всех внешних сил системы.
-- главный вектор всех внешних сил системы.
Теорема о движении центра масс имеет два следствия, которые определяют закон сохранения движения центра масс.
 Рисунок 18
Рисунок 18
|
1. Если главный вектор всех внешних сил, действующих на систему, равен нулю, то центр масс системы будет находиться в покое или двигаться равномерно и прямолинейно.
В автомобиле (рис. 18) действие газов на поршень двигателя является внутренней силой. Внешние силы – это сила тяжести автомобиля  , нормальна реакция дороги
, нормальна реакция дороги 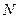 , сила трения
, сила трения 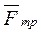 между колесами автомобиля и дороги. При отсутствии сцепления колес с дорогой (
между колесами автомобиля и дороги. При отсутствии сцепления колес с дорогой (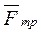 =0) действие внутренних сил не может изменить закона движения центра масс. Если
=0) действие внутренних сил не может изменить закона движения центра масс. Если 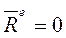 ,
, 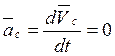 , то поэтому
, то поэтому 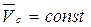 . При начальной скорости центра масс
. При начальной скорости центра масс  , центр масс будет оставаться в покое.
, центр масс будет оставаться в покое.
2. Если сумма проекций всех внешних сил, действующих на систему, на какую-либо ось равна нулю, то проекция скорости центра масс на данную ось будет оставаться постоянной. Если 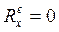 , то
, то 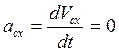 , поэтому
, поэтому  . Если в начальный момент времени
. Если в начальный момент времени  , то учитывая, что
, то учитывая, что  , координата центра масс остается постоянной (xc=const). Для человека, стоящего на абсолютно гладкой горизонтальной поверхности (рис. 19), внешними силами является его вес
, координата центра масс остается постоянной (xc=const). Для человека, стоящего на абсолютно гладкой горизонтальной поверхности (рис. 19), внешними силами является его вес 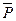 и нормальная реакция
и нормальная реакция 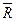 . Сила трения на гладкой поверхности отсутствует, т.е.
. Сила трения на гладкой поверхности отсутствует, т.е. 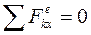 , xc=const.На гладкой поверхности человек может подпрыгнуть в вертикальном направлении, так как в проекции на ось у теорема о движении масс
, xc=const.На гладкой поверхности человек может подпрыгнуть в вертикальном направлении, так как в проекции на ось у теорема о движении масс
 поэтому
поэтому  >0, т.е. центр масс может переместиться по вертикали. Перемещение по горизонтали будет возможно при действии силы трения скольжения (рис. 19,б). Применяя теорему о движении центра масс, можно решать прямую и обратную задачи динамики поступательного движения в следующей последовательности:
>0, т.е. центр масс может переместиться по вертикали. Перемещение по горизонтали будет возможно при действии силы трения скольжения (рис. 19,б). Применяя теорему о движении центра масс, можно решать прямую и обратную задачи динамики поступательного движения в следующей последовательности:
имеет вид 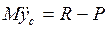 . При отталкивании от земли за счет деформации мышц R>P,
. При отталкивании от земли за счет деформации мышц R>P,
1. выбрать систему координат;
2. изобразить все внешние силы;
3. записать теорему о движении центра масс в проекции на ось координат;
4. определить искомые величины в соответствии с условиями задачи.
ПРИМЕР 10.
Определить действие фундамента кривошипного пресса при холостом ходе, если кривошип ОА=r вращается с постоянной угловой скоростью 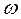 , длина кривошипа АВ=
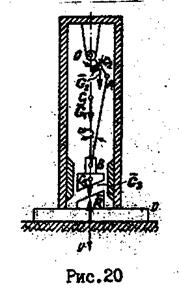
, длина кривошипа АВ= 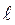 , вес фундамента и корпуса G1, вес кривошипа G2, вес штампа В G3. В начальный момент кривошип занимал вертикальное нижнее положение (рис. 20).
, вес фундамента и корпуса G1, вес кривошипа G2, вес штампа В G3. В начальный момент кривошип занимал вертикальное нижнее положение (рис. 20).
РЕШЕНИЕ.
1. На пресс действуют внешние силы: сила тяжести корпуса с фундаментом 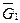 , кривошипа
, кривошипа  , штампа
, штампа 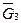 и нормальная реакция грунта
и нормальная реакция грунта 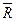 .
.
 2. Запишем теорему о движении центра масс системы в проекции на ось у:
2. Запишем теорему о движении центра масс системы в проекции на ось у: 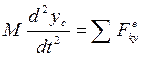 , (1) где
, (1) где 
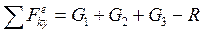 . (2)
. (2)
3. Выразим ординату ус центра масс 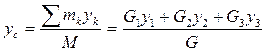 , (3) где G=G1+G2+G3.
, (3) где G=G1+G2+G3.
Угол поворота кривошипа  .
.
y1=OC1=const;
y2=OC2cos 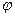 =0,5rcos
=0,5rcos  ;
;
y3=OAcos 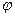 +ABcos
+ABcos 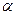 +BC3=2cos
+BC3=2cos  +
+ 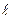 cos
cos 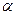 +BC3; где ВС3=const.
+BC3; где ВС3=const.
Из  ОАВ:
ОАВ: 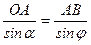 ;
; 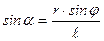 ;
; 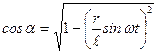 .
.
Если разложить  в ряд, отбросив члены ряда, содержащие
в ряд, отбросив члены ряда, содержащие 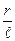 в степени выше второй, получим
в степени выше второй, получим 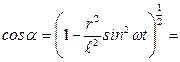 ~
~ 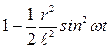 ; тогда
; тогда 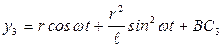 ;
; 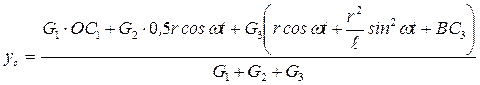 . (4)
. (4)
Продифференцируем (4) дважды по времени и подставим в (1)  ; (5)
; (5)

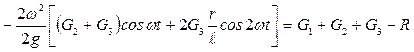 ; отсюда находим нормальную реакцию грунта, а следовательно, величину давления на фундамент в зависимости от угла поворота кривошипа
; отсюда находим нормальную реакцию грунта, а следовательно, величину давления на фундамент в зависимости от угла поворота кривошипа 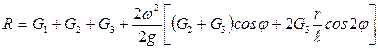 .
.
ПРИМЕР 11.
Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1=18кг, движущейся вдоль горизонтальных направляющих, и груза D массой m2=6кг. В момент времени t0=0, когда плита двигалась со скоростью u0=2м/с, груз начал двигаться вдоль желоба в соответствии с уравнением S=AD=0,4sin( t2) (S—в метрах, t—в секундах (рис. 21)). Определить скорость плиты в момент времени t1=1с.
t2) (S—в метрах, t—в секундах (рис. 21)). Определить скорость плиты в момент времени t1=1с.
 РЕШЕНИЕ.
РЕШЕНИЕ.
1. Внешними силами, действующими на систему, являются вес пластины 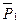 , вес груза
, вес груза 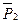 и нормальная реакция поверхности
и нормальная реакция поверхности 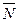 .
.
2. Применим теорему о движении центра масс в проекции на ось х:  . (1) Так как
. (1) Так как 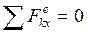 ,
,  , то
, то  . (2)
. (2)
3. Выразим произведение  , где х1, х2 – абсциссы плиты и груза.
, где х1, х2 – абсциссы плиты и груза. 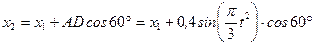 . Тогда
. Тогда  . (3) Продифференцируем (3) по времени
. (3) Продифференцируем (3) по времени  , (4) где
, (4) где  -- искомая скорость плиты.
-- искомая скорость плиты.
При t=0 u1=u0; 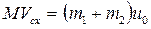 .
.
Следовательно, С1=(m1+m2)u0. (5) С учетом (2), (4) и (5) получим 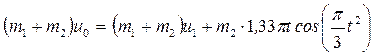 , откуда находим скорость плиты
, откуда находим скорость плиты  .
.
При t1=1c 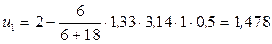 м/с.
м/с.
Date: 2015-09-24; view: 1184; Нарушение авторских прав