
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Колебания груза, подвешенного на пружине
|
|
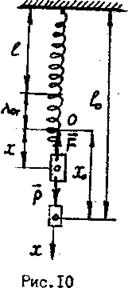
В недеформированном состоянии пружина имеет длину l (рис. 10). Если к концу пружины подвесить груз, пружина растянется на длину 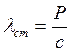 , где
, где  -- статическое удлинение пружины, зависящее от веса груза и упругих свойств пружины.
-- статическое удлинение пружины, зависящее от веса груза и упругих свойств пружины.
|
|
Так как 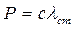 , уравнение (5.11) имеет вид
, уравнение (5.11) имеет вид  , т.е. действие постоянной силы
, т.е. действие постоянной силы 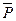 не изменяет характера колебательного движения (см. уравнение (5.2)).
не изменяет характера колебательного движения (см. уравнение (5.2)).
Если груз прикреплен к двум пружинам с жесткостью С1 и С2, то их заменяют одной пружиной с эквивалентной жесткостью, зависящей от соединения пружин. При последовательном соединении пружин (рис. 11)
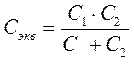 . (5.12)
. (5.12)
При параллельном соединении пружин (рис. 11)
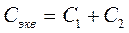 . (5.13)
. (5.13)
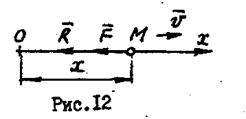
Если на точку кроме восстанавливающей силы (рис. 12) действует сила линейного сопротивления
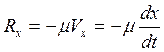 , то дифференциальное уравнение движения точки будет
, то дифференциальное уравнение движения точки будет 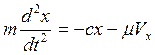 . (5.14)
. (5.14)

|
 Рисунок 11
Рисунок 11
|
|
1. В случае малого сопротивления при n<k точка совершает затухающие колебания по следующему закону
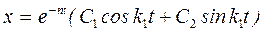 , (5.16)
, (5.16)
или 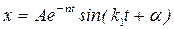 , (5.17)
, (5.17)
где С1, С2 или А, 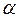 -- постоянные интегрирования, определяемые из начальных условий С1=х0;
-- постоянные интегрирования, определяемые из начальных условий С1=х0;  ; (5.18)
; (5.18)
 ;
; 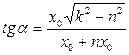 . (5.19)
. (5.19)
Период затухающих колебаний  . (5.20)
. (5.20)
Убывание амплитуды затухающих колебаний определяется декрементом

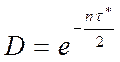 . (5.21)
. (5.21)
График затухающих колебаний располагается между двумя огибающими:  и
и 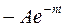 (рис. 13).
(рис. 13).

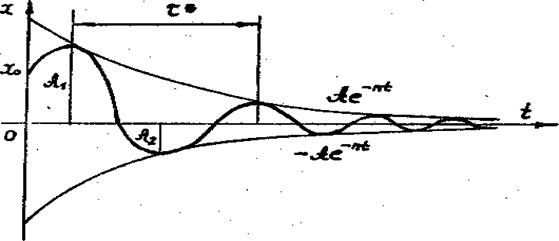
Рисунок 13
2. При n>k имеем случай большого сопротивления, точка совершает апериодическое (непериодическое) затухающее движение согласно уравнению
 , (5.22)
, (5.22)
где 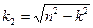 .
.
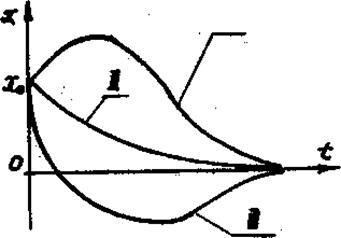 Рисунок 14
Рисунок 14
|
|
Во всех трех случаях движение быстро затухает.
3. При n=k будет случай критического (предельного) сопротивления. Точка совершает затухающее апериодическое движение по закону
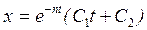 (5.23)
(5.23)
или после определения постоянных интегрирования
 . (5.24)
. (5.24)
Характер затухания зависит от начальных условий (рис. 14).
ПРИМЕР 7.
|
|
РЕШЕНИЕ.
1. В произвольный момент времени груз находится на расстоянии у от положения статического равновесия, принятого за начало координат. На груз действует сила тяжести 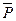 и сила упругости пружины
и сила упругости пружины 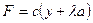 . В положении статического равновесия
. В положении статического равновесия 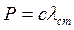 . (1)
. (1)
2. Составим дифференциальное уравнение движения груза в проекции на ось у:  (2)
(2)
или 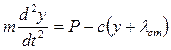 . (3)
. (3)
Тогда с учетом (1) уравнение (3) примет вид 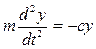 . (4)
. (4)
Разделим обе части уравнения на m и введем обозначение 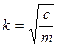 . Тогда получим
. Тогда получим 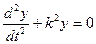 . (5)
. (5)
Решение дифференциального уравнения (5) выразим в виде y=C1coskt+C2sinkt. (6)
Постоянные интегрирования С1 и С2 определяем из начальных условий, предварительно продифференцировав по времени уравнение (6):
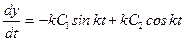 . (7)
. (7)
При t=0 у=у0 из уравнения (6): у0=С1;
из уравнения (7): V0=kС2;  .
.
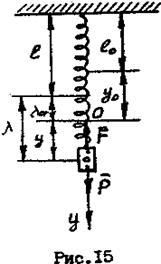
Из (рис. 15) видно, что 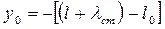 ;
;
 см;
см;  у0=-[(60+39,2)-59,2]=--40см;
у0=-[(60+39,2)-59,2]=--40см;
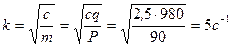 ; С1=у0= -40;
; С1=у0= -40; 
Уравнение движения груза имеет вид у=-40cos5t+40sin5t.
Период колебания груза 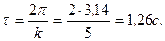
Date: 2015-09-24; view: 1641; Нарушение авторских прав
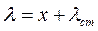 . Дифференциальное уравнение движения груза в проекции на ось х имеет вид:
. Дифференциальное уравнение движения груза в проекции на ось х имеет вид:
 (5.10)
или
(5.10)
или 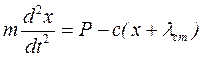 . (5.11)
. (5.11)
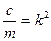 ,
, 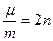 , где n – коэффициент сопротивления, то общее решение дифференциального уравнения
, где n – коэффициент сопротивления, то общее решение дифференциального уравнения
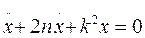 (5.15)
зависит от соотношения между коэффициентами k и n.
(5.15)
зависит от соотношения между коэффициентами k и n.
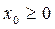 ;
;  >0;
2.
>0;
2. 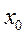 >0;
>0;  ;
3.
;
3.