Относитеельное движение точки

Законы динамики описывают абсолютное движение точки относительно неподвижной (инерциальной) системы отсчета . (6.1)

Абсолютное ускорение определяется по теореме Кориолиса 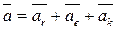, (6.2)

где 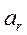-- относительное ускорение;

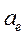-- переносное ускорение;

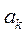-- ускорение Кориолиса.

Дифференциальное уравнение относительного движения точки имеет вид , (6.3)

где Ф_е—переносная сила инерции;

Ф_к—сила инерции Кориолиса;

; ; .

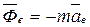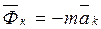Относительное движение точка совершает относительно подвижной системы отсчета. В случае переносного поступательного движения 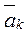=0, следовательно, =0.

Точка может находиться в состоянии относительного покоя в том случае, если соблюдается условие 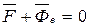, (6.4)

т.е. активные силы, приложенные к точке, уравновесятся переносной силой инерции.

Задачу динамики относительного движения материальной точки рекомендуется решать в следующем порядке:

1. определить неподвижную систему отсчета, относительно которой точка совершает абсолютное движение;

2. выделить подвижную систему отсчета, относительно которой точка совершает относительное движение;

3. рассмотреть движение подвижной системы отсчета, являющееся переносным движением для точки; по уравнению переносного движения вычислить переносное ускорение и ускорение Кориолиса, если переносное движение является вращательным;

4. записать начальные условия относительного движения точки;

5. вычислить переносную силу инерции 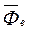и силу инерции Кориолиса ; приложить к точке силы, заданные 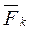и добавить силы инерци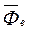и и ;

6. составить дифференциальное уравнение относительного движения точки в проекциях на подвижные оси координат;

7. проинтегрировать полученные дифференциальные уравнения; постоянные интегрирования определить по начальным условиям;

8. определить искомые величины.

ПРИМЕР 8.

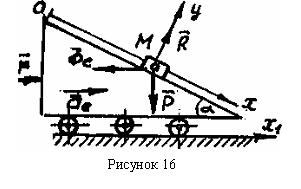
Груз массой m₁ может скользить без трения по наклонной плоскости (рис. 16), составляющей с горизонтом угол 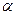. Наклонная плоскость принадлежит телу массой m₂, перемещающемуся без трения вдоль горизонтальной плоскости. С какой силой надо двигать наклонную плоскость, чтобы груз находился в состоянии покоя относительно движущегося тела?

РЕШЕНИЕ:

1. Груз М совершает относительное движение относительно подвижной системы отсчета Ох. Тележка движется под действием силы . На груз М действуют силы:

-- сила тяжести;

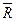-- нормальная реакция наклонной плоскости.

Приложим к грузу переносную силу инерции 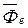. Переносная сила инерции 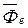направлена переносному ускорению .

2. Выразим ускорение относительного покоя груза на наклонной плоскости 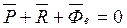. (1)

Спроецируем равенство (1) на ось х подвижной системы координат: 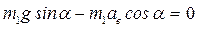. (2)

Из уравнения (2): 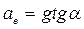. Тележка вместе с находящимся на ней грузом движется при отсутствии сопротивления по горизонтальной плоскости с ускорением . Составим уравнение движения тележки относительно неподвижной системы отсчета 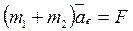, следовательно, .

ПРИМЕР 9.

Груз 1 массой m=0,4 кг укреплен на пружинной подвеске в лифте (рис. 17). Лифт движется вертикально по закону z=0,5gt² (ось z направлена по вертикали вверх; z – в метрах, t – в секундах). На груз действует сила сопротивления , где V – скорость груза по отношению к лифту, =4нс/м. Найти закон относительного движения груза при С₁=60н/м, С₂=120н/м, =0, V₀=2м/с.

РЕШЕНИЕ.

1. Заменим прикрепленные к грузу пружины, соединенные параллельно, одной эквивалентной с жесткостью С=С₁+С₂=60+120=180н/м.

2. Изобразим груз в положении, когда пружина растянута. Начало координат помещаем в положение статического равновесия. На груз действуют силы:

-- сила тяжести;

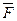-- сила упругости пружины;

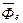-- переносная сила инерции;

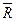-- сила сопротивления.

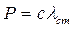; Ф_е=ma_e; .

переносное ускорение определим из закона переносного движения. По условию задачи z=0,5gt²;

; ; .

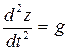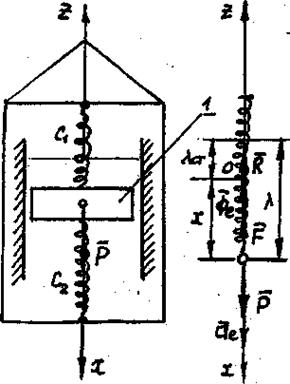Рисунок 17

3. Составим дифференциальное уравнение движения груза (1) или в проекции на ось х . (2) Разделим уравнение (2) на массу m и введем обозначения 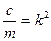; ; ; (3) или 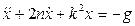. (4) Получили неоднородное дифференциальное уравнение второго порядка. Его решение х: х=х₁+х₂, где х₁ – общее решение неоднородного уравнения . (5) Решение дифференциального уравнения (5) зависит от соотношения между коэффициентами n и k. Так как в нашем случае n<k, имеем случай малого сопротивления: 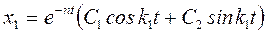, (6) где ; х₂ – частное решение уравнения (4). Так как правая часть уравнения представляет собой постоянную величину, частное решение х₂ ищем в виде х₂=В=const. Подставляем это решение в уравнение (5) и находим величину В: ;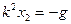

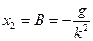. Тогда решение уравнения (4) имеет вид: 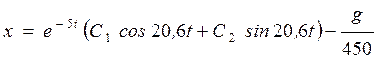. (7) Постоянные интегрирования С₁ и С₂ определяем из начальных условий. При t=0 ; x₀=V₀; ; . .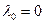

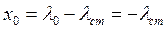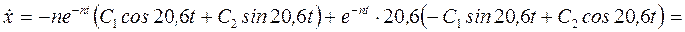
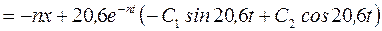При t=0 ; ; 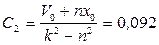; ; 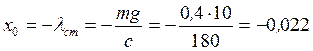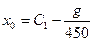Окончательно уравнение относительного движения груза имеет вид .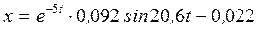

Date: 2015-09-24; view: 1036; Нарушение авторских прав