
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Моменты инерции некоторых простейших тел приведены в таблице 1
|
|
 Рисунок 32
Рисунок 32
|
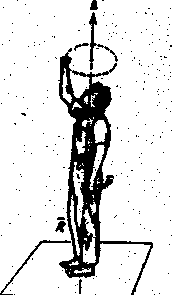 Рисунок 33
Рисунок 33
|
|
|
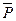 вращается вокруг вертикальной оси (рис. 32), то
вращается вокруг вертикальной оси (рис. 32), то 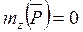 , следовательно,
, следовательно,  .
.
ПРИМЕР 16.
Однородная круглая платформа радиусом R=1м, массой m1=20кг вращается с угловой скоростью 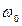 =10с-1 вокруг вертикальной оси, отстоящей от центра платформы на расстоянии ОС=в=0,5R (рис. 34). В момент времени t0=0 по желобу платформы начинает двигаться под действием внутренних сил груз D массой m2=8кг по закону S=AD=5t2, где S— в метрах, t— в секундах. Одновременно начинает действовать пара сил с моментом М=10кНм. Определить, пренебрегая массой вала, угловую скорость платформы как функцию времени.
=10с-1 вокруг вертикальной оси, отстоящей от центра платформы на расстоянии ОС=в=0,5R (рис. 34). В момент времени t0=0 по желобу платформы начинает двигаться под действием внутренних сил груз D массой m2=8кг по закону S=AD=5t2, где S— в метрах, t— в секундах. Одновременно начинает действовать пара сил с моментом М=10кНм. Определить, пренебрегая массой вала, угловую скорость платформы как функцию времени.
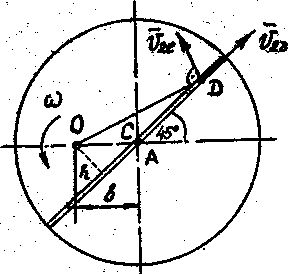 Рисунок 35
Рисунок 35
|
 Рисунок 34
Рисунок 34
|
РЕШЕНИЕ.
1. Рассмотрим механическую систему, состоящую из платформы и груза D. Применим теорему об изменении кинетического момента системы относительно оси z: 
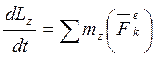 . (1) Покажем все внешние силы, действующие на систему: веса
. (1) Покажем все внешние силы, действующие на систему: веса 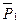 и
и 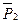 , реакции подшипника
, реакции подшипника  и подпятника
и подпятника 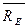 , пару сил с моментом М.
, пару сил с моментом М.
2. Кинетический момент системы относительно оси вращения найдем как сумму кинетических моментов платформы и груза 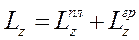 . (2) Кинетический момент платформы
. (2) Кинетический момент платформы 
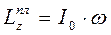 , где
, где  -- момент инерции относительно оси вращения. Для нахождения момента инерции платформы используем формулу Штейнера:
-- момент инерции относительно оси вращения. Для нахождения момента инерции платформы используем формулу Штейнера: 
 . Тогда
. Тогда 
 . (3) Кинетический момент определяем, учитывая, что груз совершает сложное движение; абсолютная скорость груза
. (3) Кинетический момент определяем, учитывая, что груз совершает сложное движение; абсолютная скорость груза 
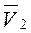 складывается из переносной
складывается из переносной 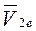 и относительной
и относительной 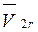 скоростей (рис. 35), т.е.
скоростей (рис. 35), т.е. 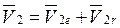 .
.
В относительном движении груз движется по платформе по закону S=5t2. Тогда  . Вектор
. Вектор  относительной скорости груза направлен вдоль желоба в сторону, соответствующую возрастанию относительной координаты S=AD (рис. 35).
относительной скорости груза направлен вдоль желоба в сторону, соответствующую возрастанию относительной координаты S=AD (рис. 35).
Переносным движением для груза является вращение платформы вокруг оси z.
 , где
, где 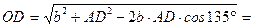
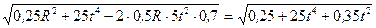 . Кинетический момент груза относительно оси вращения выразим, используя теорему Вариньона
. Кинетический момент груза относительно оси вращения выразим, используя теорему Вариньона 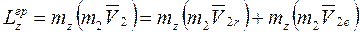 ;
;
 ;
;
где 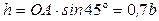 ;
;
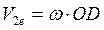 ,
,
тогда 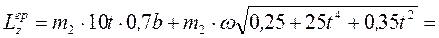
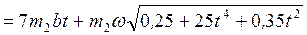 . (4) Подставим (3), (4) в (2):
. (4) Подставим (3), (4) в (2): 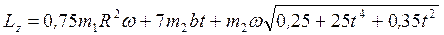 . (5)
. (5)
3. К системе приложена пара сил с моментом М=10t. Тогда уравнение (1) примет вид 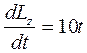 . (6) Разделяя переменные и интегрируя (6), получаем
. (6) Разделяя переменные и интегрируя (6), получаем 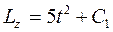 . (7) Подставим (7) в (5):
. (7) Подставим (7) в (5):
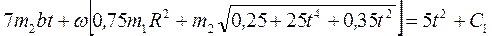 . (8) Постоянную интегрирования С1 определяем из начальных условий. Если t=0,
. (8) Постоянную интегрирования С1 определяем из начальных условий. Если t=0, 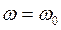 , то
, то  ;
; 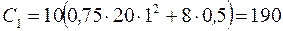 . С учетом найденного значения постоянной интегрирования из уравнения (8) выразим угловую скорость платформы
. С учетом найденного значения постоянной интегрирования из уравнения (8) выразим угловую скорость платформы 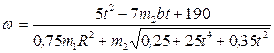 . С учетом заданных числовых значений получим
. С учетом заданных числовых значений получим  .
.
Date: 2015-09-24; view: 610; Нарушение авторских прав
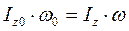 , так как внешние силы или параллельны оси (силы веса человека, гирь и платформы), или пересекает ось (реакции подшипника при отсутствии силы трения). Если человек увеличит момент инерции относительно оси вращения, разводя руки с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот.
Человек, стоящий на идеально гладкой горизонтальной плоскости (рис. 33), может повернуться вокруг оси, проходящей через центр тяжести перпендикулярно к этой плоскости, если начнет вращать руку над головой; направление вращения человека будет противоположно направлению вращения руки, так как
, так как внешние силы или параллельны оси (силы веса человека, гирь и платформы), или пересекает ось (реакции подшипника при отсутствии силы трения). Если человек увеличит момент инерции относительно оси вращения, разводя руки с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот.
Человек, стоящий на идеально гладкой горизонтальной плоскости (рис. 33), может повернуться вокруг оси, проходящей через центр тяжести перпендикулярно к этой плоскости, если начнет вращать руку над головой; направление вращения человека будет противоположно направлению вращения руки, так как 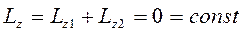 .
.