
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема об изменении количества движения
|
|
Количество движения мерой механического движения, если механическое движение перейдет в механическое. Например, механическое движение бильярдного шара (рис. 22) до удара переходит в механическое движение шаров после удара. Для точки количество движения равно произведению 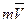 .
.
Мерой действия силы в этом случае является импульс силы
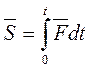 . (9.1)
. (9.1)
Импульс определяет действие силы 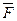 за промежуток времени
за промежуток времени 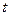 . Для материальной точки теорему об изменении количества движения можно использовать в дифференциальной форме
. Для материальной точки теорему об изменении количества движения можно использовать в дифференциальной форме 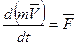 (9.2) или интегральной (конечной) форме
(9.2) или интегральной (конечной) форме 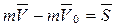 . (9.3)
. (9.3)
Изменение количества движения материальной точки за какой-то промежуток времени равно импульсу всех сил, приложенных к точке за то же время.
 Рисунок 22 Рисунок 22
|
При решении задач теорема (9.3) чаще используется в проекциях на координатные оси 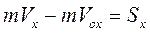 ;
;
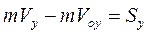 ; (9.4)
; (9.4)
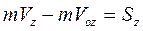 .
.
С помощью теоремы об изменении количества движения точки можно решать задачи, в которых на точку или тело, движущееся поступательно, действуют силы постоянные или переменное, зависящие от времени, а в число заданных и искомых величин входят время движения и скорости в начале и конце движения. Задачи с применением теоремы решаются следующей последовательности:
1. выбирают систему координат;
2. изображают все действующие на точку заданные (активные) силы и реакции;
3. записывают теорему об изменении количества движения точки в проекциях на выбранные оси координат;
4. определяют искомые величины.
ПРИМЕР 12.
Молот весом G=2т падает с высоты h=1м на заготовку за время t=0,01с и производит штамповку детали (рис. 23). Определить среднюю силу давления молота на заготовку.

|
|
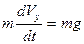 . (2)
. (2)
Разделим переменные, проинтегрируем дважды уравнение (2):  ;
;
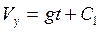 ;
;
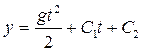 . Постоянные интегрирования С1, С2 найдем из начальных условий. При t=0 Vy=0, тогда С1=0; у=0, тогда С2=0. Следовательно, молот движется по закону
. Постоянные интегрирования С1, С2 найдем из начальных условий. При t=0 Vy=0, тогда С1=0; у=0, тогда С2=0. Следовательно, молот движется по закону 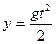 , (3) а скорость движения молота изменяется по закону
, (3) а скорость движения молота изменяется по закону 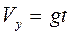 . (4) Время движения молота выразим из (3) и подставим в (4)
. (4) Время движения молота выразим из (3) и подставим в (4) 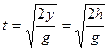 ;
; 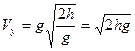 . (5)
. (5)
4. Проекцию импульса внешних сил на ось у найдем по формуле:  . (6) Подставим (5) и (6) в (1):
. (6) Подставим (5) и (6) в (1):  , откуда находим реакцию опоры, и, следовательно, искомое давление молота на заготовку
, откуда находим реакцию опоры, и, следовательно, искомое давление молота на заготовку  т.
т.
 Рисунок 24
Рисунок 24
|
Количество движения механической системы можно определить как сумму количеств движения точек системы 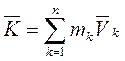 . (9.5) Количество движения системы или твердого тела можно определить, зная массу системы и скорость центра масс
. (9.5) Количество движения системы или твердого тела можно определить, зная массу системы и скорость центра масс 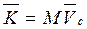 , (9.6)
, (9.6)
Изменение количества движения механической системы за некоторый промежуток времени равно сумме импульсов внешних сил, Действующих за то же время. Иногда удобнее пользоваться теоремой об изменении количества движения в проекции на оси координат 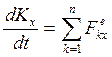 ; (9.8)
; (9.8) 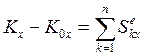 . (9.9)
. (9.9)
Закон сохранения количества движения устанавливает, что при отсутствии внешних сил количество движения механической системы остается постоянным. Действие внутренних сил не может изменить количества движения системы. Из уравнения (9.6) видно, что при 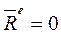 ,
,  .
.
Если  , то
, то 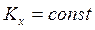 или
или  .
.
|

Применение теоремы об изменении количества движения позволяет исключить из рассмотрения все внутренние силы.
ПРИМЕР 13.
На железнодорожной платформе, свободно стоящей на рельсах, установлена лебедка А с барабаном радиуса r (рис. 26). Лебедка предназначена для перемещения по платформе груза В массой m1. Масса платформы с лебедкой m2. Барабан лебедки вращается по закону  . В начальный момент времени система была подвижна. Пренебрегая трением, найти закон изменения скорости платформы после включения лебедки.
. В начальный момент времени система была подвижна. Пренебрегая трением, найти закон изменения скорости платформы после включения лебедки.
 РЕШЕНИЕ.
РЕШЕНИЕ.
1. Рассмотрим платформу, лебедку и груз как единую механическую систему, на которую действуют внешние силы: сила тяжести груза 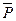 и платформы
и платформы 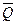 и реакции
и реакции 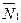 и
и 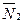 .
.
2. Так как все внешние силы перпендикулярны оси х, т.е. 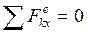 , применим закон сохранения количества движения механической системы в проекции на ось х:
, применим закон сохранения количества движения механической системы в проекции на ось х: 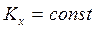 . В начальный момент времени система была неподвижна, следовательно,
. В начальный момент времени система была неподвижна, следовательно, 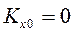
Выразим количество движения системы в произвольный момент времени. Платформа движется поступательно со скоростью 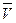 , груз совершает сложное движение, состоящее из относительного движения по платформе со скоростью
, груз совершает сложное движение, состоящее из относительного движения по платформе со скоростью 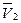 и переносного движения вместе с платформой со скоростью
и переносного движения вместе с платформой со скоростью 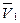 .
. 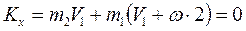 , откуда
, откуда 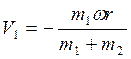 . Платформа будет перемещаться в сторону, противоположную относительному движению груза.
. Платформа будет перемещаться в сторону, противоположную относительному движению груза.
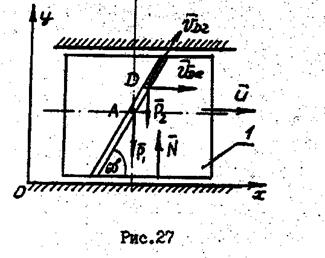
ПРИМЕР 14.
|
|
 t2) (S—в метрах, t—в секундах), (рис. 26). Определить скорость плиты в момент времени t1=1с, используя теорему об изменении количества движения механической системы.
t2) (S—в метрах, t—в секундах), (рис. 26). Определить скорость плиты в момент времени t1=1с, используя теорему об изменении количества движения механической системы.
где  ,
,  -- количество движения пластины и груза соответственно.
-- количество движения пластины и груза соответственно. 

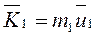 ;
; 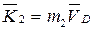 , где
, где  --абсолютная скорость груза D. Из равенства (1) следует, что К1х+К2х=С1 или m1ux+m2VDx=C1. (2) Для определения VDx рассмотрим движение груза D как сложное, считая его движение по отношению к пластине относительным, а движение самой пластины переносным, тогда
--абсолютная скорость груза D. Из равенства (1) следует, что К1х+К2х=С1 или m1ux+m2VDx=C1. (2) Для определения VDx рассмотрим движение груза D как сложное, считая его движение по отношению к пластине относительным, а движение самой пластины переносным, тогда 
 , (3)
, (3) 
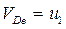 ;
; 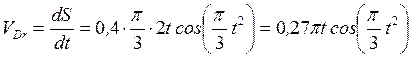 или в проекции на ось х:
или в проекции на ось х: 

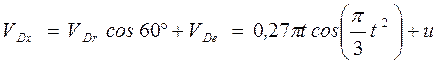 . (4) Подставим (4) в (2):
. (4) Подставим (4) в (2): 
 . (5) Постоянную интегрирования С1 определим из начальных условий: при t=0 u=u0; (m1+m2)u0=C1. (6) Подставляя значение постоянной С1 в уравнение (5), получаем
. (5) Постоянную интегрирования С1 определим из начальных условий: при t=0 u=u0; (m1+m2)u0=C1. (6) Подставляя значение постоянной С1 в уравнение (5), получаем 
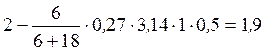 м/с.
м/с.
Date: 2015-09-24; view: 1371; Нарушение авторских прав
 и реакция опоры
и реакция опоры 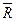 . Величина опорной реакции изменяется со временем, поэтому рассмотрим среднее ее значение
. Величина опорной реакции изменяется со временем, поэтому рассмотрим среднее ее значение 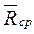 .
2. направим ось координат у по вертикали вниз и применим теорему об изменении количества движения точки в проекции на эту ось:
.
2. направим ось координат у по вертикали вниз и применим теорему об изменении количества движения точки в проекции на эту ось: 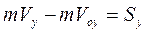 , (1) где
, (1) где  -- скорость молота в конце удара;
-- скорость молота в конце удара;
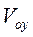 -- начальная скорость молота в момент соприкосновения с заготовкой.
3. Для определения скорости
-- начальная скорость молота в момент соприкосновения с заготовкой.
3. Для определения скорости  составим дифференциальное уравнение движения молота в проекции на ось у:
составим дифференциальное уравнение движения молота в проекции на ось у:
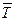 , так как перед выпрыгиванием кальмара сила
, так как перед выпрыгиванием кальмара сила 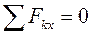 , тогда
, тогда 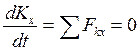 , откуда
, откуда 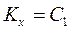 . (1)
2. Выразим проекцию количества движения на ось х для рассматриваемой механической системы
. (1)
2. Выразим проекцию количества движения на ось х для рассматриваемой механической системы 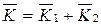 ,
,