Теорема об изменении момента количества движения

Количество движения материальной точки 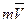является величиной векторной, для которой можно определить момент относительно 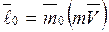центра или оси: ; . (10.1) Производная по времени от момента количества движения точки относительно центра или оси равна моменту действующей силы относительно того же центра или оси: 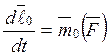, (10.2) 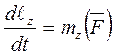. (10.3)

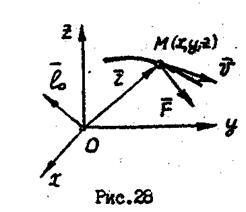
Момент количества движения называют еще кинетическим моментом. Кинетический момент точки 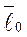приложен в точке О, относительно которой он определяется (рис. 28).

Если момент силы, приложенной к точке, относительно какого-либо центра или оси равен нулю, то кинетический момент точки относительно этого центра или оси остается постоянным. Если , то ;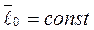

Если 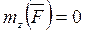, то 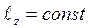. (10.4)

ПРИМЕР 15.

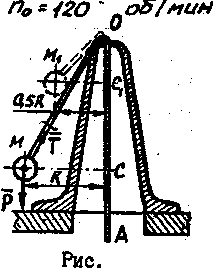
Гирька М привязана к концу нерастяжимой нити (рис. 29), часть которой ОА пропущена через вертикальную трубку; гирька движется вокруг этой трубки по окружности радиуса МС=R, делая n₀=120об/мин. Медленно втягивая нить ОА в трубку, укорачивают наружную часть до длины ОМ₁, при котором гирька описывает окружность радиуса R₁=0,5R. Сколько оборотов в минуту делает гирька по этой окружности?

РЕШЕНИЕ.

1. Применим теорему об изменении кинетического момента относительно оси. Принимаем гирьку за материальную точку, и приложим к ней силу тяжести 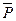и реакцию связи – натяжение нити 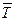. Так как сила 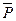параллельна оси z, а сила 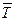пересекает эту ось, то , следовательно, кинетический момент точки относительно оси z будет оставаться постоянным. Согласно (10.4) .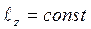

2. В начальный момент времени гирька двигалась по окружности радиуса R, совершая n₀=120об/мин. Определим кинетический момент гирьки относительно оси z, обозначив массу гирьку m и предварительно выразив скорость гирьки через число оборотов 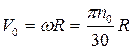, тогда 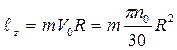. При втягивании нити радиус уменьшился до R₁=0,5R, а кинетический момент относительно оси остался постоянным. Следовательно, 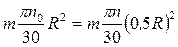, откуда 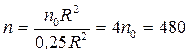об/мин.

Для механической системы кинетический момент (или главный момент количества движения системы относительно какого-либо центра или оси) равен сумме кинетических моментов точек системы относительно того же центра или оси ;

. (10.5)

Для вращающегося твердого тела кинетический момент относительно оси вращения равен произведению угловой скорости на его момент инерции относительно оси вращения.

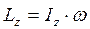. (10.6)

Момент инерции является мерой инертности для вращающихся тел. Моментом инерции механической системы из n точек относительно произвольного центра или оси называется сумма произведений масс этих точек на квадраты их расстояний до соответствующего центра или оси, т.е. 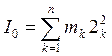; (10.7)

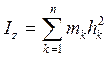. (10.8)

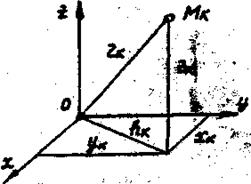Рисунок 30

	Для тел сложной геометрической формы вводится понятие радиуса инерции, т.е. расстояния до точки, где нужно сосредоточить массу тела, чтобы момент инерции этой точки относительно какого-либо центра или оси был равен моменту инерции тела относительно того же тела или оси. . (10.9)

Теорема Гюйгенса-Штейнера устанавливает зависимость между моментами инерции относительно параллельных осей:

момент инерции твердого тела или механической системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс плюс произведение массы на квадрат расстояния d между осями 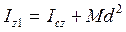. (10.10)

Для однородного стержня длиной 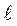(рис. 31) моменты инерции относительно центра и оси определяют по формулам:

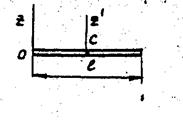Рисунок 31

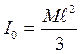; (10.14)

. (10.12)

Формула (10.12) наглядно иллюстрирует изменение теорему

Штейнера: .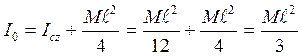

К точкам механической системы приложены внешние и внутренние силы.

Первая производная по времени от кинетического момента системы относительно произвольного центра или оси равна сумме моментов внешних сил, действующих на систему относительно того же центра или оси (теорема об изменении кинетического момента). 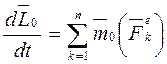; (10.13)

. (10.14)

Если момент внешних сил системы относительно произвольного центра или оси равен нулю, то кинетический момент системы относительно того же центра или оси остается постоянным:

1. Если , то .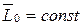

2. Если 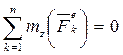, то . ()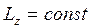

Date: 2015-09-24; view: 481; Нарушение авторских прав