
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

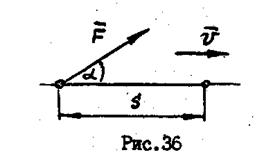
Работа и мощность силы
|
|
|
|
|
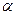 <
<  ), работа будет положительной, а сила называется движущей. Например, сила тяги
), работа будет положительной, а сила называется движущей. Например, сила тяги 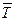 двигателя автомобиля (рис. 37).
двигателя автомобиля (рис. 37).
|
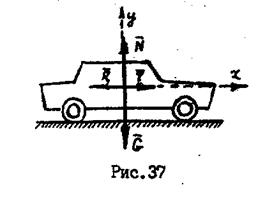
Если сила перпендикулярна перемещению,  , то такая сила работы не совершает. Например, работа сил
, то такая сила работы не совершает. Например, работа сил  и
и 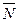 (рис. 37) равна нулю, так как сила перпендикулярна перемещению.
(рис. 37) равна нулю, так как сила перпендикулярна перемещению.
Если работу совершает переменная сила или точка приложения силы перемещается по криволинейной траектории (рис.38),
|
 Рисунок 38
Рисунок 38
|
где 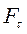 -- проекция силы на касательную;
-- проекция силы на касательную;
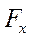 ,
,  ,
, 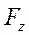 --проекции сил на оси декартовых координат;
--проекции сил на оси декартовых координат;
 ,
, 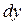 ,
, 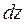 -- дифференциалы координат точки приложения силы.
-- дифференциалы координат точки приложения силы.
Выражение (11.5) называется аналитическим выражением элементарной работы. Чтобы определить полную работу силы на перемещении М1М2 точки ее приложения, необходимо проинтегрировать выражение (11.2) 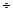 (11.5) в соответствующих пределах. Например,
(11.5) в соответствующих пределах. Например, 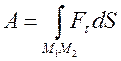 . (11.6)
. (11.6)
Одну и ту же работу можно произвести за различное время. Величину, характеризующую быстроту приращения работы, называют мощностью
 . (11.7) Используя выражения элементарной работы (11.2)
. (11.7) Используя выражения элементарной работы (11.2) 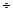 (11.5), можно получить формулы для вычисления мощности силы:
(11.5), можно получить формулы для вычисления мощности силы: 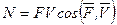 ; (11.8)
; (11.8)
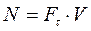 ; (11.9)
; (11.9)
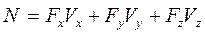 . (11.10)
. (11.10)
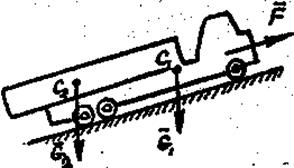 Рисунок 39
Рисунок 39
|
|
Работа силы тяжести равна произведению силы тяжести на вертикальное перемещение ее точки приложения h:  . (11.11)
. (11.11)
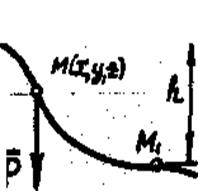 Рисунок 40
Рисунок 40
|
|
Так как точке О соответствует положение статического равновесия, координаты х0 и х1 представляют собой начальную и конечную деформации пружины, поэтому формула (11.12) примет вид: 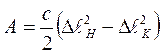 , (11.13)
, (11.13)
| |||
|
Работа постоянного момента силы, приложенного к телу, вращающемуся вокруг неподвижной оси z, равна произведению этого момента на изменение угла поворота 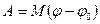 . (11.14)
. (11.14)
 Рисунок 42
Рисунок 42
|
|
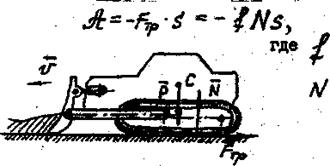 Рисунок 43
Рисунок 43
|
Работа силы трения всегда отрицательна, так как сила трения направлена противоположно движению (рис. 43).
|
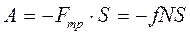 , (11.15)
, (11.15)Date: 2015-09-24; view: 505; Нарушение авторских прав
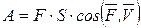 , (11.1)
где
, (11.1)
где 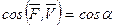 - косинус угла между
направлением силы и направлением
перемещения.
- косинус угла между
направлением силы и направлением
перемещения.
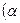 >
> 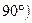 , сила, оказывая сопротивление движению, совершает отрицательную работу и называется силой сопротивления. К таким силам относятся сила резания, сила трения, сила сопротивления воздуха (рис. 37) и другие, которые всегда направлены в сторону, противоположную движению.
, сила, оказывая сопротивление движению, совершает отрицательную работу и называется силой сопротивления. К таким силам относятся сила резания, сила трения, сила сопротивления воздуха (рис. 37) и другие, которые всегда направлены в сторону, противоположную движению.
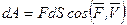 , (11.2) В зависимости от характера действующих сил элементарную работу можно вычислить по следующим формулам:
, (11.2) В зависимости от характера действующих сил элементарную работу можно вычислить по следующим формулам:
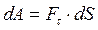 ; (11.3)
; (11.3)
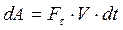 ; (11.4)
; (11.4)
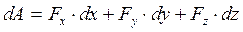 , (11.5)
, (11.5)
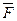 можно получить, уменьшив скорость путем включения низшей передачи.
можно получить, уменьшив скорость путем включения низшей передачи.
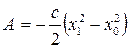 или
или 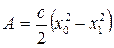 . (11.12)
. (11.12)
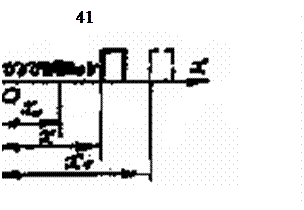
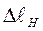 ,
,  -- соответственно начальная и конечная деформация пружины (рис. 41).
-- соответственно начальная и конечная деформация пружины (рис. 41).
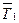 и
и 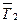 , которые при вращении шкива создают момент
, которые при вращении шкива создают момент 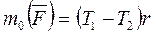 . За время t шкив повернется на угол
. За время t шкив повернется на угол 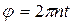 . Тогда работа вращающегося момента будет рассчитана по формуле:
. Тогда работа вращающегося момента будет рассчитана по формуле: 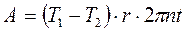 , где Т1-Т2 – разность натяжений ведущей и ведомой ветви передачи.
, где Т1-Т2 – разность натяжений ведущей и ведомой ветви передачи.