
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение второй задачи динамики
|
|
Для нахождения закона движения точки по заданным силам необходимо дважды проинтегрировать дифференциальные уравнения движения точки, составленные в проекциях на соответствующие координатные оси. Постоянные интегрирования определяются по начальным условиям. В случае прямолинейного движения составляется одно дифференциальное уравнение движения в проекции на ось, совпадающую с направлением движения точки:
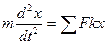 , (4.1)
, (4.1)
где 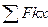 -- сумма проекций всех сил, приложенных к точке, на координатную ось.
-- сумма проекций всех сил, приложенных к точке, на координатную ось.
Уравнение (4.1) можно представить в виде
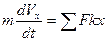 (4.2)
(4.2)
и проинтегрировать дважды.
В решение уравнения входят две произвольные постоянные, которые находятся из начальных условий:
t=0, Vx=V0, x=x0.
За начальный момент времени принимается момент начала движения точки под действием заданных сил, для которого известны положение точки и ее скорость.
Введение начальной скорости учитывает влияние на ее движение сил, действующих на материальную точку до того времени, который принят за начальный момент времени. Например, скорость электровоза в момент начала торможения, принимается за начальный момент, учитывает результат действия на него силы тяги и силы трения о поверхность рельсов до момента выключения реостата.
при решении второй задачи динамики применительно к материальной точке необходимо придерживаться следующей последовательности:
1. изобразить точку в текущий момент времени;
2. показать активные силы, действующие на точку;
3. освободить точку от связей, заменяя их действие соответствующими реакциями;
4. выбрать систему координат; начало координат следует поместить в начальном положении точки, и оси координат направить так, чтобы координаты точки и проекции ее скорости на эти оси в текущий момент времени были положительными, если точка движется прямолинейно, то координатную ось следует направить вдоль траектории движения; если точка движется по криволинейной траектории, то целесообразно использовать естественную систему координат, совместив начало координат с текущим положением точки и направив касательную к траектории так, чтобы для текущего положения точки естественная координата и проекция скорости точки на касательную были положительными;
5. найти сумму проекций всех сил, действующих на точку, на выбранные оси координат;
6. составить дифференциальные уравнения движения точки;
7. проинтегрировать дифференциальные уравнения соответствующим методом, зависящим от вида полученных уравнений;
8. установить начальные условия движения материальной точки;
9. определить произвольные постоянные интегрирования;
10. подставить произвольные постоянные в результат интегрирования, выразив затем уравнение движения точки.
Произвольные постоянные интегрирования можно определять по мере их появления. В некоторых случаях при интегрировании дифференциальных уравнений удобно пользоваться определенными интегралами.
Рассмотрим решение второй (основной) задачи динамики для случаев прямолинейного движения точки под действием следующих сил:
а. сила постоянна по модулю;
б. сила зависит от времени;
в. сила зависит от положения точки;
г. сила зависит от скорости.
ПРИМЕР 3.
Груженый самосвал начинает спускаться с горы с выключенным двигателем (рис. 4), имея начальную скорость V0=10м/с. Найти, за какое время автомобиль закончит спуск, если длина участка l=1000м, коэффициент трения f=0,2, 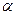 =
= 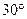 .
.
РЕШЕНИЕ.
1. Принимаем автомобиль за материальную точку и изображаем ее в текущий момент времени.

|
2. Изображаем силы, действующие
на точку:
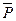 -- вес автомобиля с грузом.
-- вес автомобиля с грузом.
Реакцию шероховатой опорной
поверхности раскладываем на две
составляющие:
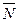 -- нормальное давление;
-- нормальное давление;
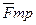 -- сила трения скольжения;
-- сила трения скольжения;
Fтр=fN, N=Pcos  , Fтр=fPcos
, Fтр=fPcos 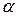 .
.
3. выбираем систему координат, как показано на рис. 4.
4. Так как автомобиль движется по прямолинейному участку пути, составляем одно дифференциальное уравнение движения в проекциях на ось x:
 (1)
(1)
или  . (2)
. (2)
После сокращения m и разделения переменных получим
dVx=g(sin 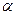 -fgcos
-fgcos 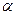 )dt. (3)
)dt. (3)
Интегрируя дважды полученное уравнение, получаем:
Vx=g(sin 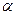 -fgcos
-fgcos 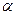 ) t C1; (4)
) t C1; (4)
x=g(sin 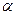 -fgcos
-fgcos 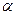 )
) 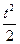 +C1t+C2. (5)
+C1t+C2. (5)
5. Начальные условия движения:
при t=0, V0=10м/с, х0=0.
6. Определяем произвольные постоянные С1 и С2, подставляя начальные условия в уравнения (4) и (5):
из уравнения (4): V0=C1;
из уравнения (5): С2=0.
7. Следовательно, закон движения автомобиля на наклонном участке пути имеет вид
x=g(sin 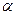 -fgcos
-fgcos 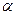 )
) 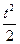 +V0t. (6)
+V0t. (6)
Зная пройденный автомобилем путь, равный l, находим время движения t1:
при t=t1 x=l;
1000=9,81(sin 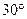 -
-  )
)  +10t1
+10t1
или 0,16 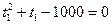 . (7)
. (7)
Решая квадратное уравнение (7), получаем:
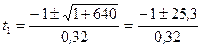 ;
;
t1=75,9 с.
ПРИМЕР 4.
Машинист тепловоза начинает тормозить на прямолинейном участке пути (рис. 5), когда тепловоз имеет скорость V0. Сколько времени будет двигаться тепловоз до полной остановки и какой пройдет путь, если сила торможения пропорциональна времени  (a—постоянный коэффициент).
(a—постоянный коэффициент).
РЕШЕНИЕ.
1. Так как тепловоз движется поступательно, можно рассматривать движение одной его точки, считая, что к ней приложены все заданные силы: сила тяжести  , нормальная реакция рельсов
, нормальная реакция рельсов 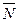 и сила торможения
и сила торможения 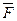 .
.
2. За начало отсчета принимаем момент начала торможения, когда скорость тепловоза V=V0.
3. Составим дифференциальное уравнение движения точки в проекции на ось x:
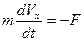 (1)
(1)
или  . (2)
. (2)
Разделим уравнение (2) на m и, разделив переменные, дважды проинтегрируем
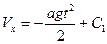 ; (3)
; (3)
 . (4)
. (4)
3. Определим постоянные интегрирования по начальным условиям при t=0, Vx=V0, x0=0;
из уравнения (1) получим C1=V0;
из уравнения (2): С2=0.
4. Следовательно, закон движения тепловоза на участке торможения имеет вид
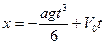 . (5)
. (5)
5. Время торможения 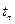 найдем из уравнения (3) при условии, что в конце участка торможения скорость тепловоза равна 0.
найдем из уравнения (3) при условии, что в конце участка торможения скорость тепловоза равна 0.
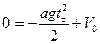 , откуда
, откуда 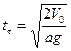 .
.
Длину участка торможения найдем из уравнения (5)
 .
.
ПРИМЕР 5.
Глубину реки измеряют грузом, опускаемым в воду до дна реки. При скорости груза V0 трос оборвался, и груз достиг дна через t секунд после момента обрыва троса.
Определить пройденный грузом путь Н, если при движении груз испытывает сопротивление Rx=-kmV, где m—масса груза, k—постоянный коэффициент. Силой выталкивания груза из воды пренебречь.
РЕШЕНИЕ.
1. За начало отсчета принимаем точку О, соответствующую положению груза в момент обрыва троса. Ось х направим в сторону движения груза.
2. Покажем все силы, действующие на груз во время движения в сопротивляющейся среде: силу тяжести 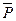 и силу сопротивления
и силу сопротивления 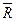 , направленную противоположно скорости груза.
, направленную противоположно скорости груза.
3. Составим дифференциальные уравнения движения груза в проекции на ось х:
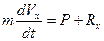 (1)
(1)
или  . (2)
. (2)
 Рисунок 6
Рисунок 6
|


Разделим уравнение (2) на m и проинтегрируем, разделяя переменные
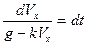 ,
,
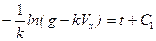 . (3)
. (3)
Определим постоянную интегрирования С1, принимая во внимание, что при t=0 Vx=V0,
 . (4)
. (4)
С учетом (4) уравнение (3) примет вид 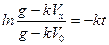 . (5)
. (5)
Откуда 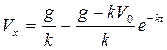 . (6)
. (6)
Уравнение (6) устанавливает зависимость скорости движения груза в сопротивляющейся среде от времени. Заменяя 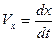 и разделяя переменные, получаем:
и разделяя переменные, получаем:
 . (7)
. (7)
После интегрирования уравнения (7) получим
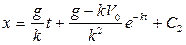 . (8)
. (8)
Постоянную интегрирования С2 определим из начальных условий. При t=0 x=x0, С2=  , тогда уравнение (8) имеет вид
, тогда уравнение (8) имеет вид
 . (9)
. (9)
Путь Н, пройденный грузом, найдем из условия, что при t=T x=H, тогда
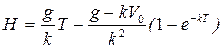 .
.
Дифференциальные уравнения описывают движение материального объекта до тех пор, пока на него действуют силы, входящие в правую часть этих уравнений. Если в какой-либо момент времени действие этих сил изменяется или прекращается, то для описания последующего движения нужно составлять новые дифференциальные уравнения движения. Начальными условиями нового движения будут скорость и координаты тела в конце предшествующего движения.
ПРИМЕР 6.
Груз D массой m=4,5кг, получив в точке А начальную скорость V0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости (рис. 7). Участок АВ наклонен к горизонтали под углом  , участок ВС горизонтальный.
, участок ВС горизонтальный.
На участке АВ на груз кроме силы тяжести действует постоянная сила Q=9Н и сила сопротивления  . В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на тело кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила Fx=3sin(2t).
. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на тело кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила Fx=3sin(2t).
Считая груз материальной точкой и зная время его движения на участке АВ t1=3c, найти закон движения груза на участке ВС.
РЕШЕНИЕ.
|
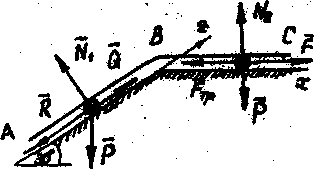 Рисунок 7
Рисунок 7
|
или 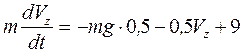 . (3)
. (3)
Разделим обе части уравнения (3) на m и введем обозначения
 ;
; 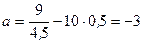 ;
; 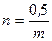 ;
; 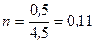
Тогда уравнение (3) примет вид  . (4)
. (4)
Разделив переменные и проинтегрировав уравнение (4), получим
 ;
;  . (5)
. (5)
При t=0 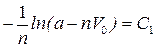 ;
;
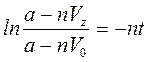 ;
;  .
.
При t=t1 Vz=VB, т.е.  м/с.
м/с.
2. Рассмотрим движение точки на участке ВС. Составим дифференциальное уравнение движения точки в проекции на ось х:
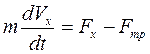 (6)
(6)
Fтр=fN2, где N2=P. Тогда  (:m)
(:m)
 . (7)
. (7)
При t=0 Vx=VB;
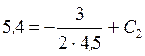 ; С2=5,77.
; С2=5,77.
Тогда 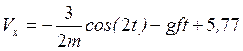 . (8)
. (8)
Учитывая, что 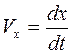 и разделяя переменные, получаем
и разделяя переменные, получаем
 ;
;
 .
.
При t=0 x=0, C3=0. Тогда
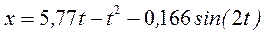 .
.
Date: 2015-09-24; view: 2488; Нарушение авторских прав
 , (1)
, (1)
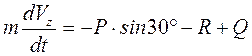 (2)
(2)