Анализ взаимосвязи признаков

Условное распределение. Совместное «поведение» двух признаков. Таблица сопряженности. Показатели таблицы сопряженности. Маргинальные частоты. Сравнение структуры условных распре­делений. Типы задач, решаемых посредством таблиц сопряженно­сти. Типологический синдром. Типологическая группа. Зависимый ¾ независимый признаки. Направленная ¾ ненаправленная связь. Ста­тистическая зависимость ¾ статистическая независимость. Силь­ная ¾ слабая связь. Меры связи. Функциональная ¾ корреляционная связь. Линейная ¾ нелинейная связь. Локальные ¾ глобальные меры связи. Непосредственная ¾ опосредованная связь. Истинное ¾ лож­ное значения меры связи.

Независимо от выбранной стратегии анализа (восходящей или нисходящей) и после изучения, условно говоря, «поведения» от­дельно взятых признаков, естественным образом возникает необхо­димость анализа взаимосвязи, взаимодействия между признаками. Будем рассматривать только случай двух признаков. Анализ «пове­дения» двух признаков — совместного или относительно друг друга — социологу необходим для поиска ответа на вопросы типа: суще­ствует ли связь между этими признаками; влияет ли один признак на другой; можно ли, зная значение одного из них, сделать вывод относительно значения другого и т. д. Если гипотезы о взаимосвязях были предварительно сформулированы, то речь может пойти по проверке этих гипотез.

Является очевидным, что поиск ответов на подобные вопросы может осуществляться с помощью условных распределений. В самом простом случае сравниваются одномерные распределения одного из признаков, полученные для разных совокупностей объектов, на которых второй из признаков принимает одно из своих значений. Возможно также изучать и как бы совместное «поведение» этих признаков.

В качестве исходных для анализа признаков рассмотрим при­знаки «будущая профессия студента» и «степень удовлетворенно­сти студента учебой». Одномерные распределения этих признаков нам уже известны. Мы будем иметь представление о совместном «поведении» или поведении этих признаков относительно друг дру­га, если получим так называемую таблицу сопряженности (корре­ляционную таблицу). Таковой является таблица 3.3.1. Строки в ней соответствуют шести будущим профессиям (политологи, социоло­ги, культурологи, филологи, психологи и историки), пронумерованным по порядку (они соответствуют профессиональным группам 1, 2, 3, 4, 7, 8 из таблицы 3.2.1), а столбцы ¾ пяти степеням удовлетворенности учебой. Пересечения столбцов и строк образу­ют ячейки (клетки) таблицы. В нашем случае число таких ячеек равно 6 x 5 = 30. В ячейках таблицы могут содержаться значения раз­личных показателей. Это ¾ характеристики группы студентов, отне­сенных к ячейке, т. е. студентов с определенной будущей профес­сией, имеющих определенную степень удовлетворенности учебой.

В последней строке представлено распределение (одномерное, простое) студентов по степени их удовлетворенности учебой (часто­ты обозначены как n_0j), а в последнем столбце ¾ распределение сту­дентов по их будущим профессиям (n_j0). Для этих частот в контексте анализа таблиц сопряженности есть особое название. Эти частоты называют маргинальными частотами, и для их обозначения исполь­зуется, как видите, двойной индекс. В последней строке ¾ маргиналь­ные частоты по столбцам, а в последнем столбце ¾ маргинальные частоты по строкам. Естественно, они совпадают с данными таблиц 3.2.1 и 3.2.2. Сумма маргинальных частот обозначена (n₀₀) и равна 1000, т. е. равна числу наших студентов-гуманитариев.

Любая ячейка таблицы, соответствующая группе объектов, удов­летворяющих условию строки и столбца, может содержать четыре показателя, характеризующих эту группу. К примеру, ячейка (1,2) соответствует 20-ти политологам со второй степенью удовлетворен­ности учебой (скорее неудовлетворен, чем удовлетворен). Точнее, тем, кто ответил на оба заданных вопроса. Как мы уже знаем, число ответивших может не совпадать с числом опрошенных. Чтобы не было путаницы, будем считать, что таблица сопряженности получена для некоторой идеальной подвыборки (в нашем случае каж­дый студент ответил на каждый вопрос). Для обозначения ее объе­ма будем пользоваться понятием ¾ общее число объектов.

Таблица 3.3.1

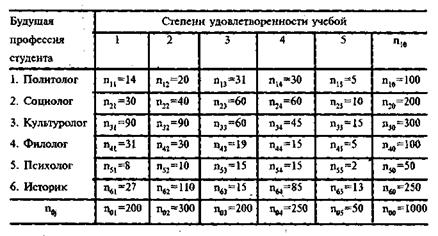
Для политологов, имеющих вторую степень удовлетвореннос­ти учебой, абсолютная частота равна п₁₂. Кроме нее в ячейку (1,2) можно поместить и значения других показателей, а именно отно­сительных частот либо в долях (частости), либо в процентах. При этом таких частот может быть три. Назовем абсолютную частоту первым показателем в ячейке таблицы сопряженности и будем исходить из того, что относительные частоты рассчитываются в долях. Тогда второй показатель будет равен доле этих n₁₂ студен­тов в общем числе n₀₀, студентов-гуманитариев. Третий показатель ¾ доля этих же n₁₂ студентов среди n₁₀ студентов-политологов. Чет­вертый ¾ доля этих же п₁₂ студентов среди n₀₂ студентов, степень удовлетворенности учебой которых равна двум.

Таблица 3.3.2

Таблица сопряженности: относительные частоты

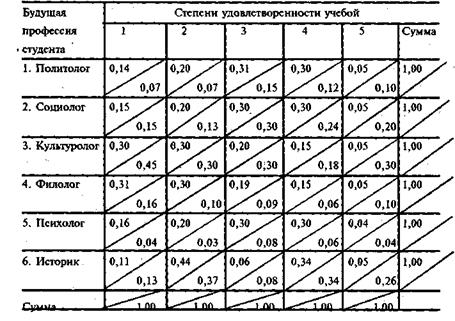
Теперь запишем все это в общем виде (в виде формул) для объек­тов любой природы и для любой (i, j)-й ячейки таблицы сопряжен­ности. Число объектов, удовлетворяющих условию i -и строки и j -го столбца, равно n_ij общее число объектов равно n₀₀. Маргиналь­ные частоты по столбцам ¾ n_0j, а маргинальные частоты по стро­кам ¾ n_i0. Символ «нуль» обозначает, что по тому индексу, на месте которого он стоит, проведено как бы суммирование или усредне­ние или расчеты проведены без учета некоторого признака. Это очень удобный способ для обозначений частот разного вида, воз­никающих при анализе таблицы сопряженности. Вместо этого сим­вола можно использовать и другой, например, точку или звездочку. «Точка», «звездочка», «нуль» ¾ общепринятые в литературе симво­лы для обозначения маргинальных частот.

Таким образом, (i, j)-и ячейке таблицы сопряженности можно поставить в соответствие четыре показателя:

1. nij ¾ число объектов, удовлетворяющих условию i-й строки и j-ro столбца;

2. n_ij / n₀₀ ¾ доля их в общей совокупности объектов;

3. n_ij / n_i0 ¾ доля их в совокупности объектов, удовлетворяющих условию строки;

4. n_ij / n_0j ¾ доля этих же объектов в совокупности объектов, удовлетворяющих условию столбца.

Социолог анализирует «поведение» одного признака относи­тельно другого с помощью двух последних показателей. В таблице 3.3.2 приведены в каждой ячейке значения этих двух показателей для нашей задачи. Над чертой в ячейке доля по строке, а под чер­той ¾ доля по столбцу. На основе этих данных социолог может ре­шать два типа задач.

Во-первых, он может сравнивать структуру «удовлетвореннос­ти учебой» в различных профессиональных группах студентов. Мы упомянули новый в нашем курсе термин «структура». В самом про­стом случае под структурой «чего-то» понимается совокупность элементов этого «чего-то» и взаимосвязи между этими элементами.

Это вам знакомо. В нашем случае элементами являются различные степени удовлетворенности учебой, а в качестве взаимосвязи между ними выступает различие в «долях», соответствующих этим степе­ням. Для того чтобы представить эти структуры графически, пост­роим на одном и том же графике эмпирические кривые распреде­ления по удовлетворенности учебой отдельно для каждой профессиональной группы студентов-гуманитариев.

На рис. 3.3.1 изображены шесть эмпирических кривых распре­деления, соответствующих шести профессиональным группам. На горизонтальной Оси отложены на равном расстоянии пять степеней удовлетворенности. Чтобы построить кривую распределения для политологов (первая наша профессиональная группа), по вертикаль­ной оси откладываем следующие значения (0,14, 0,20, 0,31, 0,30, 0,05) из первой строки таблицы 3.3.2. Это доли политологов с соот­ветствующей степенью. удовлетворенности (от 1 до 5) среди всех политологов. Аналогично поступаем и в случае остальных профес­сиональных групп. К примеру, чтобы построить кривую распреде­ления для студентов-психологов, по вертикали откладываем следу­ющие значения (0,16, 0,20, 0,30, 0,30, 0,04) соответственно пяти степеням удовлетворенности учебой.

Чисто визуально из рис. 3.3.1 можем сделать следующие выво­ды. Структура удовлетворенности «похожа» у политологов, соци­ологов и психологов. Эти группы образуют как бы один типологи­ческий синдром, составляют одну и ту же типологическую группу по структуре удовлетворенности. Структура удовлетворенности при­мерно одинакова у культурологов и филологов. Это уже второй типологический синдром. Таким образом, можно утверждать на­блюдаем наличие трех типологических синдромов при анализе структуры удовлетворенности. Третий из них ¾ специфическая и отличная от других структура удовлетворенности учебой студен­тов-историков. Эти синдромы, типологические образования и есть специфические эмпирические закономерности, требующие от со­циолога объяснения. В целом можно констатировать, что будущая профессия студента влияет на удовлетворенность учебой или де­терминирует эту удовлетворенность. На вопрос, каким образом, мы тоже ответили пока без каких-либо количественных оценок. Как видите, в этом случае визуализация распределений имеет для социолога огромное значение.

Выше упоминали два типа задач, решаемых с помощью табли­цы сопряженности. Первый тип мы с вами рассмотрели. Формаль­но мы анализировали третий показатель таблицы сопряженности. Другой из этих типов задач для нашего примера заключается в срав­нении профессиональной структуры в различных по степени удов­летворенности учебой группах студентов. На рис. 3.3.2 изображены пять эмпирических кривых распределения в соответствии с этими

Date: 2015-09-24; view: 518; Нарушение авторских прав