Анализ характера «поведения» признака

Эмпирическая кривая распределения. Показатели средней тенден­ции для различных типов шкал. Дескриптивная статистика. Мода. Медиана. Среднее арифметическое значение, взвешенное среднее. Меры рассеяния вокруг средних. Дисперсия. Коэффициент вариа­ции как мера однородности. Квартильный размах. Меры качествен­ной вариации. Коэффициент качественной вариации. Среднее гео­метрическое. Энтропия.

Регулярно на экране телевизора вы видите визуально представ­ленные распределения какого-нибудь признака (столбики с обозначением процентов). Например, результаты изучения обществен­ного мнения по претендентам на президентский пост или место в парламенте. Эти картинки называются гистограммами ¾графи­ческое изображение или визуализация распределений. Они стро­ятся по определенным правилам и в основном нужны не столько самому социологу, сколько заказчику социологического исследо­вания (красиво и наглядно). Социологу они нужны лишь на предварительном этапе работы с эмпирией для того, чтобы на компь­ютере быстро просмотреть характер распределений. Существует множество способов визуализации. Например, в работе [2] при­водится 15 способов визуального изображения (графики, диа­граммы) одних и тех же данных ¾ одномерного распределения признака.

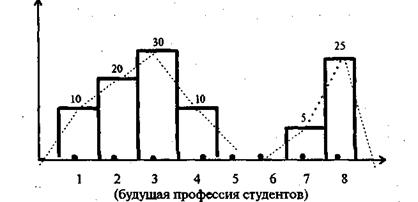
На рис. 3.2.1 изображена гистограмма, соответствующая распределению студентов по будущим профессиям. На горизонтальной оси, начиная с любой точки, откладываются на равном расстоянии восемь (см. таблицу 3.1.1) профессий. Над каждой «профессией» воздвигается столбик высотой равный относительной частоте этойпрофессии. Столбики могут отстоять друг от друга и на каком-то расстоянии. В нашем случае они примыкают друг к другу. Гистог­рамму можно строить по частостям или по процентам. Они совпа­дут при соответствующем выборе масштаба. Для этого на верти­кальной оси одна и та же точка должна соответствовать либо единице, либо ста процентам.

Сумма площадей всех прямоугольников равна единице, если "'' она построена по частостям и равна ста, если гистограмма пост­роена по процентам. Вертикальная ось служит только для задания масштаба, поэтому гистограмму начинают строить с любой пози­ции по горизонтали. Ломаная линия (обозначенная на рис. 3.2.1 пунктиром) называется эмпирической кривой распределения, или полигоном. Она соединяет середины верхней стороны прямоуголь­ников. Эта кривая и ее характеристики говорят социологу о «по­ведении» признака. Второй из этих терминов мало употребляется на практике.

Процент/частость/

Рис. 3.2.1 Гистограмма и эмпирическая кривая распределения студентов по профессиональным группам

Аналогичным образом строится гистограмма и эмпирическая кривая распределения для второго признака, т. е. для распреде­ления студентов по степени их удовлетворенности учебой. Они изображены на рис. 3.2.2. Если для номинальных и порядковых шкал гистограммы эмпирическая кривая распределения служит только для визуализации, то для метрических они имеют особый смысл.

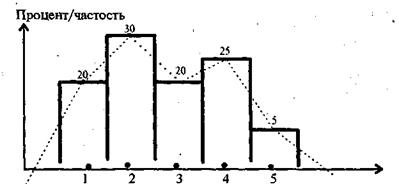
(степени удовлетворенности учебой студентов)

Рис. 3.2.2 Гистограмма и эмпирическая кривая распределения по степени удовлетворенности учебой

Построим гистограмму и эмпирическую кривую распределения для признака «продолжительность затрат времени на учебу». В этом случае гистограмма строится несколько иначе. Как вы заметили, каждый столбик гистограммы по площади был равен числу респон­дентов. Визуально передается не высота столбика, а его площадь. Ширина столбика равнялась единице и для номинального, и для порядкового признаков. В данном случае ширину нельзя выбрать одинаковой, так как наши интервалы разные. Поэтому гистограм­ма строится по плотности распределения. Плотность в интервале -это число респондентов, приходящихся на единицу интервала. Обо­значим плотность в наших шести интервалах через

Р₁, Р₂, Р_з, Р₄, P₅, Р₆

Тогда Р₁ = 27/1 = 27; Р₂= 75/1,5 = 50; Р_з= 150/1,5 = 100;

Р₄ = 348/3 = 116; Р₅ = 250/1 = 250; Р₆ = 150/1 = 150

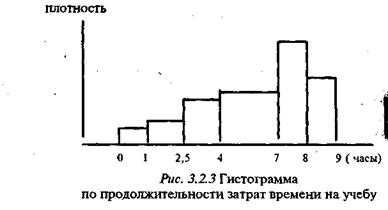
В данном случае эмпирическая кривая распределения не име­ет содержательного смысла, ибо не передает характера распреде­ления. Поэтому такую кривую строят при делении на равные ин­тервалы. Число интервалов при этом определяется уже исходя из формальных критериев. Для порядковой и метрической шкалы гистограмму и эмпирическую кривую распределения можно пост­роить и по накопленной частоте. Только в этом случае для эмпи­рической кривой распределения существует специфическое назва­ние. Она называется кумулята, а накопленную частоту называют кумулятивной. Построим ее по данным, представленным в табли­це 3.2.1.

Таблица 3.2.1

Распределение по продолжительности учебы (равные интервалы)

На рис. 3.2.4 изображены гистограмма и кумулята по продолжительности затрат времени на учебу (интервалы равные, их де­вять). Кумулята ¾ это всегда возрастающая кривая. Пока на пунк­тирные линии не обращайте внимания.

Графическое изображение распределений в виде эмпирических кривых распределения (полигоны и кумуляты) нужны социологу в зависимости от типа шкал для разных целей. Для номинальной шкалы мы можем упорядочить (провести ранжирование) различ­ные профессиональные группы по их представительности (объему) в наших данных и соответственно выделить модальные (самые боль­шие по объему) группы. Для порядковой шкалы, кроме этого, оп­ределяется и степень единодушия студентов в оценке своей удов­летворенности учебой. Вспоминаем шкалу Терстоуна, для Построения которой посредством медианы и квартального размаха оценивалась степень единодушия экспертов. Самую важную роль играют эмпи­рические кривые распределения для метрических признаков. Но эта роль связана не с первичным анализом и не с изучением пове­дения эмпирических индикаторов, а с анализом поведения показателей/коэффициентов/ индексов.

При статистическом подходе к анализу распределений каждый такой показатель теоретически может иметь закон распределения с определенными параметрами и по эмпирической кривой распределения можно судить о том, каков этот закон. Знание законов дает воз­можность применения к анализу эмпирии всего богатства средств, накопленных в математической статистике. Законов очень много, и отсюда названия: нормальный закон распределения (рис. 3.2.5), лога­рифмический закон распределения (рис. 3.2.6), линейный закон распре­деления (рис. 3.2.7) и т.д. Законы вы проходили и в школе. Уравнение прямой, параболы, гиперболы интерпретируются как математичес­кие законы, связывающие две величины Х и Y. Некоторые законы нельзя записать в явном виде, т. е. в виде математической формулы.

Что касается самого факта существования закона распределения какого-то показателя, то это требует доказательства. Например, в виде проверки статистических гипотез. Эту тему относим к после­дующим этапам в вашем образовании.

Перейдем к рассмотрению характеристик, описывающих (от­сюда название дескриптивная статистика) «поведение» признака в целом, в виде некоторой эмпирической тенденции. Потому они и называются мерами центральной тенденции.

Мода

Наиболее часто встречающееся значение признака называется модой. Таких значений может быть и несколько. В нашем случае третья профессия является модальной. Социолог никогда не рабо­тает с одной единственной модой, а употребляет понятие «модаль­ные значения». Для нашего примера профессии 3 и 8 являются модальными. Аналогична ситуация в случае порядковых шкал. Мода равна 2 (наиболее часто встречаются студенты, степень удовлетво­ренности учебой которых равен двум). В качестве модальных зна­чений имеет смысл рассматривать все же два значения, 2 и 4, т. е. наиболее распространены две группы по степени удовлетвореннос­ти. И это несмотря на то, что по объему они различны. Однако по сравнению с другими группами они достаточно большие. Можно считать, что наличие таких модальных групп специфично, харак­терно, типично для изучаемой совокупности студентов-гуманита­риев. Это самая простая эмпирическая закономерность.

Нахождение модального значения в случае метрической шкалы невозможно по рис. 3.2.3, ибо ширина интервалов различна и это модальное значение может находиться в любом интервале. Поэто­му прежде всего возникает задача определения модального интерва­ла ¾интервала, содержащего моду. Для этого необходимо перейти от деления на интервалы, основанного на содержательных крите­риях, к делению на интервалы по формальным критериям. При этом интервалы должны иметь равную длину и их число должно зависеть от степени изменчивости признака. Чем больше степень изменчивости, тем больше нужно интервалов для определения модального. На рис. 3.2.8 приведена гистограмма, построенная для случая деления «продолжительности» на девять равных интерва­лов. Абсолютные частоты в этих интервалах были приведены выше в таблице 3.2.1. Плотность в каждом интервале пропорциональна этим абсолютным частотам. Ширина интервала равна 1. Эмпири­ческая кривая распределения в этом случае называется эмпиричес­кой функцией распределения плотности.

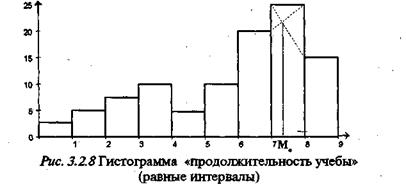
Существует математическая формула для вычисления моды, но мы приведем лишь геометрический способ нахождения моды в модальном интервале. Модальным интервалом является интервал в 7—8 часов. Значение моды вычисляется геометрически (пересе­чение пунктирных линий на рис. 3.2.8) и примерно равно 7,3 часа (см. стрелочку на том же рисунке). Является логичным, что мода должна находиться ближе к тому концу модального интервала, ко­торый примыкает к интервалу с большим числом объектов. Возни­кает вопрос, как подсчитать значение моды, если модальный ин­тервал первый или последний по счету. Тогда за моду принимается середина этих интервалов.

Модальные значения определенным образом говорят о харак­тере поведения признака и в основном о числе «горбов». Напри­мер, вспоминаем задачу ранжирования по предпочтениям различ­ных сортов пива. С какими ситуациями мы сталкивались? С достаточным единодушием (один горбик, одна мода), с двумя про­тивоположными тенденциями (два горбика, две моды) и с полным разнообразием (практически равномерное распределение ¾ моды нет). Чтобы как-то продвинуться в анализе предпочтений, мы использо­вали еще одну характеристику ¾ медиану, к рассмотрению которой и переходим.

Date: 2015-09-24; view: 378; Нарушение авторских прав