Среднее арифметическое

Для любой совокупности значений признака это сумма всех значений, деленная на их число. Вернемся к примеру признака ¾ продолжительность затрат времени на учебу. Обозначим число сту­дентов-гуманитариев через n (для нашего случая n=1000), а че­рез X_i: — значение этой продолжительности для i-го студента. Тогда средняя арифметическая продолжительности будет равна:

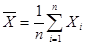
Таким образом можно определить среднею продолжительность затрат времени на учебу в группах студентов с любой «будущей профессией», с любой степенью удовлетворенности учебой и т. д.

Социолог часто встречается с ситуацией, когда конкретные зна­чения признака по отдельным объектам неизвестны. Исходно име­ются только интервалы изменения признака и частота (абсолютная или относительная) встречаемости объектов в этих интервалах. На­пример, та же продолжительность может быть задана в виде интер­валов и частоты в них. Это может быть в двух случаях. Первый ¾ данные о продолжительности получены c помощью прямого воп­роса анкеты: «Сколько времени Вы в среднем в неделю тратите на занятия, связанные с учебой?». При этом предлагаются заданные заранее интервалы. По сути, мы имеем дело с порядковой шкалой. В этом случае также можно вычислить среднее значение продолжи­тельности для некоторой группы студентов. Только она называется средняя взвешенная и вычисляется несколько по-другому.

Второй случай, когда у социолога отсутствуют конкретные зна­чения по каждому объекту в ситуации вторичного анализа. Вторич­ным анализом социолог называет анализ «чужих» данных для реше­ния своих собственных, новых задач. Тогда часто приходится работать уже с вычисленными до него средними арифметическими. Например, результаты исследования бюджетов времени обычно публикуются в виде средних затрат времени с указанием объема группы, для которой они получены. В процессе вторичного анализа возникает необходимость объединения каких-то групп и, соответ­ственно, в подсчете общей средней. В этой ситуации также необхо­дима средняя взвешенная для вычисления «средней средних».

Вычислим среднюю продолжительность затрат времени на уче­бу студентами-гуманитариями по данным таблицы 3.1.3. Для этого предполагается, что продолжительность для каждого респондента, отнесенного к интервалу, равна середине интервала. Для наших шести интервалов их середины соответственно равны:

Х₁ = 0,5; X₂ = 1,75; X₃ = 3,25; X₄ = 5,5; X₅ = 7,5; X₆ = 8,5.

Нам известно число студентов в каждом интервале:

n₁ = 27; n₂ = 75; n₃ = 150; n₄ = 348; n₅ = 250; n₆ = 150.

Тогда продолжительность затрат времени на учебу в среднем на студента или средняя взвешенная продолжительность равна:

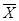= (0,5x27+1,75х75+3,25х150+5,5х348+7,5х250Н-8,5х150)/1000=5,7

Формула для вычисления средней взвешенной выглядит для k интервалов следующим образом:

,

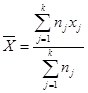где X_j ¾ середина j -го интервала.

Аналогично вычисляется «средняя средних». Допустим, перед социологом стоит задача вычисления средней продолжительности жизни мужчин в России по данным отдельных областей. Эти дан­ные представляют собой среднюю продолжительность жизни муж­чин по каждой области. Естественно, «среднюю средних» вычис­ляем с весами, равными численности мужчин в каждой области.

Все рассмотренные характеристики: мода, медиана, средняя арифметическая, среднее взвешенное ¾ являются средними. Они характеризуют центральные тенденции одномерного распределения. Есть и другие средние, но они в социологии применяются редко. Поэтому среднюю арифметическую называют просто средней, а мода и медиана сохраняют свои названия. Без процедуры усреднения социолог-эмпирик существовать не может. Другое дело, с помо­щью каких средних он проводит эту процедуру.

Сами по себе значения «средних» мало о чем говорят, если социолог не видит эмпирическую кривую распределения, напри­мер, на экране компьютера. В ситуации «невидения» ему помогают интерпретировать любые средние так называемые меры вариации, меры рассеяния объектов вокруг этих средних. Сначала мы рассмот­рим меру вариации для случая метрической шкалы, а затем для порядковой и номинальной.

Прежде чем перейти к этой проблеме, заметим, что любая средняя характеризует центральную тенденцию распределения толь­ко тогда, когда объекты в основном сосредоточены вокруг этих средних, т.е. изучаемая совокупность объектов однородна относи­тельно признака. Однородность ¾ это очень важное понятие для всех, кто работает с эмпирией. Социолог сталкивается с проблемой однородности в разных контекстах. Как раз вот здесь пара понятий «качество ¾ количество» очень важна. Разделение понятий каче­ственная однородность и количественная однородность имеет ог­ромный смысл. Например, разве есть смысл в среднем доходе или в среднем возрасте россиянина? Конечно же, нет. И в то же время есть смысл в средней заработной плате сельских врачей или в сред­нем возрасте мужчин-пенсионеров. Необходима качественная одно­родность для того, чтобы начать анализ количественных характе­ристик распределения признака.

Сами количественные характеристики могут указывать/показы­вать на отсутствие количественной однородности по анализируемо­му признаку. Это в свою очередь будет говорить о наличии качествен­ной неоднородности.

Date: 2015-09-24; view: 382; Нарушение авторских прав