Распределение студентов по их будущей профессии

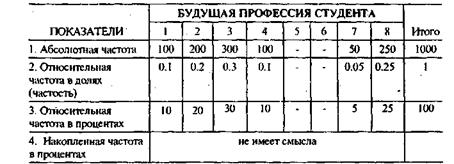
Второй показатель в таблице ¾ относительная частота в до­лях, или частость, т. е. это доля респондентов определенной про­фессии среди всех опрошенных студентов-гуманитариев. Очень ча­сто в социологических исследованиях наряду или вместо числа опрошенных используется число ответивших. Для нашего приме­ра не имеет значения, по отношению к какому «числу» считается доля, ибо число ответивших совпадает с числом опрошенных. В массовых опросах различение этих величин носит принципиаль­ный характер, так как число неответивших бывает достаточно большим. Сама же проблема неответивших является серьезной проблемой в массовых опросах. Мы касались этой проблемы при обсуждении так называемой (нами) проблемы социологического нуля. Относительная частота в долях ¾ это важный показатель для последующих этапов работы с данными.

Доля интерпретируется как оценка вероятности обладать опре­деленной профессией. Последняя фраза только для тех, кто случайно прослушал курс по теории вероятности.

Третий показатель ¾ относительная частота в процентах — определяет, какой процент респондентов будет иметь ту или иную профессию. Это самый любимый показатель социолога, и вы в этом могли убедиться, если уже успели принять участие в каком-нибудь социологическом исследовании. Процент и частость ¾составные элементы языка анализа социолога.

И наконец, четвертый показатель ¾ накопленная частота впроцентах. С такой частотой мы сталкивались при построении шкалы Терстоуна. Для номинального уровня измерения она почти никогда не имеет смысла. Чисто технически ее можно подсчитать для нашей таблицы. Это и будет маленьким примером неадекват­ности математики. Прямо говоря ¾ чушь. Отсюда и вывод, что, живя в век потрясающих компьютеров, слепо нажимать на кноп­ки для запуска «модерновых» математических методов недопус­тимо. Компьютер может подсчитать все, только есть ли в этом смысл. Вот в чем вопрос.

Накопленная частота имеет «прозрачный» содержательный смысл только для шкал начиная с порядковых. Рассмотрим рас­пределение студентов по степени их удовлетворенности учебой, полученной с помощью применения логического квадрата. В таб­лице 3.1.2 представлено распределение респондентов по степени «удовлетворенности» по тем же четырем показателям (и в этом случае цифры не реальные, а модельные). Все показатели имеют смысл. Число опрошенных так же, как и в случае первого призна­ка, совпадает с числом ответивших. Степени удовлетворенности обозначены цифрами от 1 до 5. При этом 1 соответствует мини­мальному уровню удовлетворенности, а 5 ¾ максимальному.

Таблица 3.1.2

Date: 2015-09-24; view: 371; Нарушение авторских прав