Распределение студентов по степени удовлетворенностью учебой

Напомним, какой смысл имеет накопленная частота. Напри­мер, в таблице 3.1.2 частота, равная 70%, означает, что число студентов с уровнем удовлетворенности меньше четырех составля­ет 70% от числа опрошенных, а меньше трех ¾ 50%. Перейдем к случаю метрической шкалы. Для табличного представления распределения «продолжительности» необходимо разбить диапазон ее изменения на отдельные интервалы. Важно отметить, что рас­пределение не всегда имеет смысл представлять в табличной фор­ме, так как деление на интервалы не всегда имеет смысл, напри­мер, для динамических рядов или для продолжительности затрат времени в исследованиях бюджета времени. Это происходит пото­му, что можно сразу переходить к изучению характеристик, опи­сывающих характер распределения. Необходимо иметь также в виду, что признак может носить дискретный характер (встречают­ся только целые числа) или непрерывный характер (встречаются числа, имеющие целую часть и дробную). С непрерывностью встре­чаемся в основном при работе с аналитическими индексами на этапе анализа эмпирий.

Наш третий признак ¾ продолжительность затрат времени на учебу ¾ может носить дискретный характер, если выражен в мину­тах, и непрерывный характер ¾ если выражен в часах. Остановим­ся на последнем случае. Для каждого студента этот производный показатель равен его среднесуточным (в часах) затратам времени на учебу. Введем интервалы и подсчитаем число студентов, вне­сенных в каждый интервал. В социологии в отличие от многих других наук, работающих с эмпирией, разбиение на интервалы не может носить формального характера. Такое разбиение всегда происходит в зависимости от исследовательских задач, а точнее, от того, как и для чего будет использоваться признак в процессе дальнейшего анализа. Поэтому социолог пользуется при этом понятиями «группировка данных», «типологическая группировка данных».

При выделении интервалов изменения продолжительности зат­рат времени на учебу исходим из значений максимальной и ми­нимальной продолжительности, встретившихся в нашей выборке. Разница между этими величинами называется вариационным раз­махом. Без знания минимальной продолжительности нельзя опре­делить нижнюю границу первого интервала, а без знания макси­мальной ¾ верхнюю границу последнего интервала. Допустим, в нашем случае максимум (max) равен 9-ти часам, а минимум (min) ¾ 0 часам. Последний факт можно объяснить тем, что в выборку попали студенты, которые были больны: никаких занятий, входя­щих в «продолжительность учебы», в недельном бюджете време­ни у них не было. Чтобы сей факт не вызвал недоумения, заме­тим, что сбор информации о бюджете времени студента происходит за неделю, предшествующую опросу.

Тогда наши интервалы (всего их шесть) могут выглядеть следу­ющим образом:

1. 0—1 часов;

2. 1—2,5 часов;

3. 2,5—4 часов;

4. 4—7 часов;

5. 7—8 часов;

6. 8—9 часов.

Нетрудно догадаться, из чего мы исходили при выборе имен­но таких интервалов. К примеру, в последний интервал попадут студенты ¾ «трудяги», в первый ¾ те, кто по какой-то причине был «выключен» из учебного процесса, а в четвертый ¾ модаль­ная (самая распространенная) группа студентов. Кстати, это не факт, а гипотеза, и, соответственно, она может не подтвердиться в реальном исследовании. Для наглядности на рис 3.1.1 изображе­ны эти интервалы в виде делений на линейке.

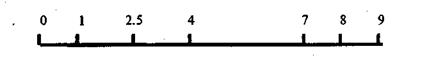
Рис 3.1.1

При отнесении респондента к конкретному интервалу по продолжительности учебы возникает такой вопрос. Куда входят ниж­няя и верхняя границы интервала? Другими словами, к какому интервалу отнести, например, студента, у которого продолжитель­ность учебы равна четырем часам. Ведь его можно отнести и к первому, и ко второму интервалу. Эта проблема решается просто. Например, социолог принимает решение, что все верхние грани­цы интервалов относятся к интервалу. Тогда студент, у которого продолжительность учебы равна 4-м часам, будет отнесен к третьему интервалу. Студент, у которого продолжительность учебы равна 8-ми часам, ¾ к пятому и т. д.

Эти же интервалы могут быть заданы и в другой форме:

1. 0—1 часов;

2. 1,1—2,5 часов;

3. 2,6—4 часов;

4. 4,1—7 часов;

5. 7,1—8 часов;

6. 8,1—9 часов.

В этом случае при вычислениях возникает другая проблема, если продолжительность учебы некоторого студента, например, равна 1,09 часов. Опять же принятие решения в руках социолога. Он может отнести к интервалу не только верхнюю границу, но и то, что ниже нижней границы следующего интервала, т.е. рес­пондент, у которого продолжительность учебы равна 1,09 часам будет отнесен к первому интервалу.

Используя первые введенные интервалы, подсчитаем по ним распределение респондентов (таблица 3.1.3.)

Обратите внимание, что каждая из приведенных таблиц имеет заголовок, итоговый столбец. Эти таблицы ¾ пример оформления как бы первичных результатов социологического исследования. Разумеется, за исключением того, что реальные таблицы содержат только один показатель из четырех приведенных. Такого рода таблицы служат и для представления результатов исследования. Эта ситуация типична для исследований общественного мнения.

Социолог называет распределение признака «линейкой», про­стым распределением, линейным распределением, частотным рас­пределением, простой группировкой, потому что речь в самом деле идет о самых простых, одномерных распределениях в отличие от ус­ловных и многомерных. Последние получаются тогда, когда одно­временно строится распределение по нескольким признакам. К слу­чаю двумерных распределений перейдем чуть позже.

Таблица 3.1.3

Date: 2015-09-24; view: 511; Нарушение авторских прав